Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 30

Некоторые замечания. 1. Критерий Колмогорова дает незавышенные оценки тогда, когда гипотетическое распределение F(x) и его параметры полностью известны заранее. На практике, если предварительно известны общий вид распределения F(x), а его параметры вычисляются по статистическим данным, то критерий Колмогорова дает излишне оптимистические оценки, и в ряде случаев рискуют принять как правдоподобную гипотезу, плохо согласующуюся с опытными данными.

2. При малом числе измерений критерий также дает излишне оптимистичные оценки. Обычно допускается использование этого критерия, когда n не менее нескольких десятков.

3. Удобен критерий для браковки нулевой гипотезы о близости  и F(x). Если по критерию гипотеза отвергается, то нет смысла проверять ее с помощью более чувствительных критериев согласия.

43

вение начального электрона и формирование разряда оказывают влияние различные случайные факторы.

Для выявления закономерностей, которым подчиняется статистическое запаздывание разряда, приложим толчком постоянное напряжение, достаточное для возникновения разряда, одновременно к n0 одинаковым искровым промежуткам, состоящим из одинаковых электродов, при одинаковой и постоянной интенсивности внешней ионизации и прочих равных условиях. Поскольку прикладывается постоянное напряжение, то t₁ = 0. Первоначально рассмотрим промежутки, у которых t_j << t_c, т.е. можно принять t_p » t_c. Пусть интенсивность появления электронов в одном промежутке, т.е. число электронов в единицу времени, равна р₁ (эта вероятность может быть названа эффективностью электрона). Тогда за интервал времени dt в промежутке появляется p₁ i dt эффективных электронов.

Обозначим через ni число тех промежутков, в которых еще не произошел разряд к моменту t, т.е. в которых статистическое запаздывание больше. В последующий интервал времени dt произойдет дополнительное число разрядов, равное уменьшению(-dn_t) числа незавершенных разрядов определяется произведением числа эффективных электронов на количество промежутков, в которых еще не совершился разряд. Отсюда

-dn_t = p₁ i n_t dt.                                    (5.33)

Разделив переменные и проинтегрировав в пределах от 0 до t и от n₀ до n_t, получаем

53

ЗАДАЧА 2. По условию задачи 1 максимальное различие между  и F(x) имеет место при Х = 3,0,  = 0,05, поэтому l = 0,05  = 1,0. Принимая уровень значимости a₁ = 0,1, по табл. 5.5 находим l_a = 1,224. Так как в рассматриваемом случае выполняется неравенство l < l_a, то гипотеза о возможности аппроксимации эмпирического закона законом равномерной плотности принимается с уровнем значимости a₁ =0.1.

КРИТЕРИЙ ПИРСОНА (критерий c²). При использовании этого критерия сравниваются статистические и теоретические рi вероятности попадания в разряды (интервалы) x_i-1, x_i. В качестве меры расхождения U используется сумма квадратов отклонений (взятых с некоторыми “весами” С_i:  где k – число разрядов. Коэффициенты С_i вводятся для того, чтобы сделать отклонения в различных разрядах равными по значимости, они принимаются равными  С_i = , где n – число измерений. При таком выражении для коэффициентов С_i учитывается значимость отклонения . Очевидно, что при малых вероятностях  одна и та же абсолютная величина  является более существенной, чем при больших величинах .К. Пирсон показал, что при больших n закон распределения случайных величины  прак

44

g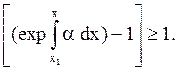                           (5.31)

Используя (5.29) и учитывая, что величина напряженности Е в точке х определяется как конфигурацией электрического поля, так и величиной приложенного к промежутку напряжения, по (5.31) можно рассчитать начальное напряжение Uо, т.е. напряжение возникновения самостоятельного разряда на данной силовой линии электрического поля; причем либо завершающийся пробоем промежутка, либо существующим в форме так называемым коронным разрядом.

ХАРАКТЕРИСТИКИ ВРЕМЕНИ ЗАПАЗДЫВАНИЯ РАЗРЯДА. Электрический разряд, возникнув в промежутке, развивается в пространстве и времени. Для анализа вероятностных характеристик времени запаздывания разряда рассмотрим газовый промежуток, в котором при воздействии напряжения происходит пробой. Тогда необходимо определенное время, имеющее следующие состовляющие: