Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 27

1. Подбор теоретического закона распределения или выравнивание статистического ряда.

2. Проверка с помощью критериев согласия гипотезы о близости теоретического и получаемого из опыта эмпирического распределения.

ПОДБОР ТЕОРЕТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ.  Наилучшее выравнивание статистического ряда – задача в значительной степени неопределенная. Класс функций обычно определяется по внешнему виду статистического распределения. При этом любая аналитическая функция f(x) должна удовлетворять основным свойствам функции распределения:

f(x) = 0,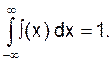       

Для определения параметров выбранного распределения применяется метод моментов. По этому методу  параметры распределения подбираются так, чтобы числовые характеристики (моменты) теоретического распределения были бы равны соответствующим оценкам числовых характеристик, рассчитанным по статистическим данным. Обычно ограничиваются четырьмя моментами: или S_k) (или E_x). Очевидно, что для симметричных распределений достаточно использовать лишь  и  . Если эмпирические распределения получаются сложными, то всегда следует стремиться выровнить статистический ряд с помощью простых функций распределения.

39

                    U₀                                                   F_пр(U)

   U_max                                                          1

   U

   U_min

                                                            y                                                          U

y₁  y₃             y₄    y₂                           U_min            U_max

Рис.5.9.Изменение U₀ по условию  Рис.5.10.Распределение напряжния                           самостоятельности разряда                       до пробоя промежутка

Дальнейшее решение связано с вычислением закона распределения функции случайной величины U_пр(y) по известному закону распределения F_эф(y) этой величины. Если F_эф(y) и U_пр(y) заданы аналитически, то для расчета имеет смысл использовать соотношения подраздела 5.1. В нашем случае более удобным является графическое определение функции распределения F_пр(y). Зафиксируем некоторое значение напряжения U, тогда F_пр(U), т. е. вероятность того, что U_пр < U, определяется следующим образом

F_пр(U) = P(U_пр < U) =          (5.39)

где нормирующй множитель

A = F_эф(y₂) – F_эф(y₁)                          (5.40)

учитывает ограничение, наложенное на пределы изменения F_пр(U) условием (5.37). Рассчитанная таким способом функция F_пр(U) показана на рис.5.10.

Пробивные напряжения различных промежутков или изоляционных конструкций измеряют при импульсном , или постоянном, или переменном напряжениях. Определение вероятности пробоя по дан

57

ЗАДАЧА 1. Проверены измерения tgd одинаковых изоляционных конструкци. Число измерений n = 400. Результаты изиерений представлены в виде несгруппированного статистического ряда в табл. 5.3. Требуется выровнить статистический ряд, принимая гипотезу о том, что закон распределения tgd равномерный.

Таблица 5.3

Диэлектрические потери одинаковых изоляционных конструкций

Таблица 5.4

Сгруппированный статистический ряд значений tgd