Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 22

Применение логнормального распределения:

1. Анализ надежности различных устройств.

2. В Технике высоких напряжений (ТВН) в электронно-ионной технологии исследование движения аэрозолей в электрическом поле, как доказано А.Н. Колмагоровым, что распределение их по размерам асимптотически стремится к логарифмическому закону. Логарифмически-нормальное распределение имеет вид по рис. 5.2.

                                      f(x)

 

                            

                                   0                              x

Рис. 5.2. Логарифмически-нормальное распределение

случайных величин

ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. Плотность распределения непрерывных случайных величин выразится: f(x) =

31

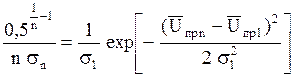,но. Тогда имеем:

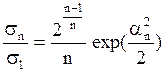                               .                             (5.51)

Обозначим s_n / s₁ = b_n. В табл. 5.10 приведена зависимость величины b, а величина s_n определяется как

                                       s_n =b_n s₁.                                      (5.52)

Из (5.49) и (5.52) следует, что увеличение числа параллельно включенных элементов в изоляционной конструкции приводит к уменьшению как среднего значения пробивных напряжений, так и их разбросов. Это задачи реальных изоляционных конструкций, изоляция секций обмотки электрической машины, конденсаторной изоляции и т.п.

ЛИТЕРАТУРА. 1.Разевиг Д. В. Методы теории вероятностей в технике высоких напряжений. – М. МЭИ, 1975. С 28 – 45, 179 – 188, 204 – 220.

2. Большев Л. Н. Таблицы математической статистики. – М. Наука, 1965. 464 с.

3. Агеева Н.Д., В.Н. Электротехническое материаловедение. /Учебн. пособие. - Вл-к. ДВГТУ,1995. 72 с.

4. Агеева Н.Д., В.Н. Электротехническое материаловедение. /Метод. указан. – Вл-к. ДВГТУ, 1995. 40 с.

65

где х ³ 0, а математическое ожидание -  и дисперсия - .

Этот закон находит применение в следующих областях.

1. В теории надежности и массового обслуживания, где плотность вероятности безотказной работы обычно описывается функцией f(x) =  а величина х характеризует время безотказной работы, тогда параметр  называется интенсивностью отказов.

 Вероятность безотказной работы в течение времени не меньше х равна     Р(Х > х) =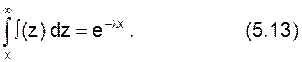

2. В физике этот закон используется для характеристики свободного пробега молекул.

3. В ТВН экспоненциальным законом описывается время статистического запаздывания разряда, как функция распределения амплитуд и крутизн токов молнии и т.д.

            Вид экспоненциального закона распределения случайных величин отображен на рис. 5.3.

f(x)

                                       l

 

0                             x

Рис. 5.3. Экспоненциальный закон распределения случайных величин

РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА. В теории надежности при изучении характеристик сроков службы аппаратуры встречаются слу

32

величинами  n, можно вычислить Ф(a_n) =  и определить по таблице нормального закона a_n = arg - эта зависимость приведена в табл. 5.10.

Таблица 5.10

Зависимости a_n и b_n от числа элементов в изделии

n	1	2	10	102	103	104	105	106
an	0	0,55	1,50	2,45	3,20	3,80	4,35	4,80
bn	1	0,81	0,58	0,40	0,33	0,28	0,25	0,20

Таким образом, значение  легко определяется по U_пр1 и s₁ и по данным табл.5.10 как

                                                                (5.49)

Отметим, что в функции не нормального закона U_0,5n – это медиана закона. Для определения sn воспользуемся (5.49) и условием нормальности F_n(U):

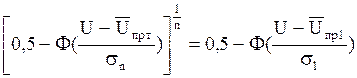              .         (5.50)

Дифференцируем обе части уравнения (5.50) по U получаем

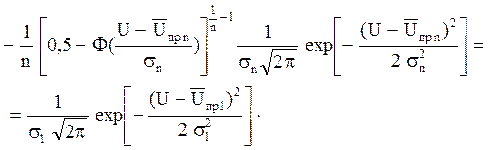
подставим U = :

64