Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 19

Интегральная функция распределения

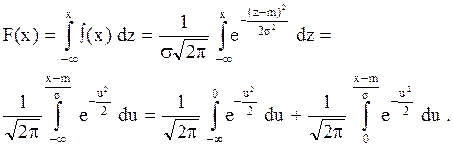
Первый интеграл равен половине интеграла Эйлера-Пуассона (5.6); второй интеграл не выражается через элементарные функции, он табулирован табл. 5.1 и носит название интеграл вероятности или функция Лапласа:

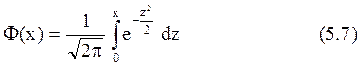
Таким образом, функция распределения случайной величины, подчиненной нормальному закону, выражается через интеграл вероятности:

Интеграл вероятности обладает следующими свойствами:

1. Ф(0) = 0, так как при х = 0 пределы интеграла (5.7) совпадают.

26

2. Ф( = 0,5, что вытекает из (5.6)

В системе координат (I_м, a_м), принимая

                                    a_м =                                     (6.4)

делит квадрат (I_м, 0, a_м) на две области  по рис. 6.5: область D, где выполняется условие U_иmax < U_i, - область С, где U_иmax > U_i – область опасного сочетания этих параметров. При этом пограничное соотношение (6.4) носит название кривой опасных параметров. Поскольку Iм и aм, образуют систему двух независимых случайных величин, то вероятность пробоя изоляции определится

                     u_иmax      u_оп = u_и                              a_м

             RI_м            La_м                                            

                                                I_м                                            I_м

Рис.6.4. Распределение                    Рис.6.5. Кривая  опасных напряжения                                         параметров на гирлянде изоляторов         

P(U_иmax > U_i) = P(I > I_м, a > a_м)    или

P(U_иmax > U_i) =

В соответствии с (6.3) имеем  f(I_м,a_м) = k_I exp(- k_I I_м) k_a exp(- k_a a_м), тогда P(U_иmax > U_i) =

= 1 -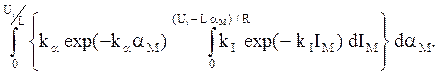

Окончательно зависимость вероятности пробоя изоляции от влияющих параметров имеет вид:

70

3. Ф(-х) = - Ф(х), что проверяется заменой переменной z = -u d в (5.7).

Таблица.5.1

Значение интеграла вероятностей Ф₀(х)

27

                                                                                          i_м

                   i_м                  u_оп                                      u_м                        L

                                    · u_пр~ 0                                                                     u_оп

R

R

Рис.6.2. ПУМ в опору ЛЭП          Рис.6.3. Схема для оценки потенциала на траверсе напряжение U_имax, приложенное к изоляции, будет превышатьее электрическую прочность: P(U_иmax > U_i). При протекании тока молнии i_м по опоре будет происходить падение напряжения на сопротивлении заземляющего устройства и на индуктивности опоры. Потенциал в точке крепления гирлянды Uоп определяется по рис. 6.3 как