Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 28

РЕШЕНИЕ. Сначала вычислим оценки матожидания и диспер

40

женности которого известен в виде силовой линии E_y(x), где х – координата на силовой линии, а y – координата на эквипотенциали. К промежутку приложено постоянное напряжение, а катод – электрод с большим радиусом кривизны. Источник внешней ионизации создает у поверхности катода эффективные электроны, вероятность появления которых задается некоторой функцией распределения F_эф(y), показанной на рис. 5.8. Приложенное напряжение медленно возF_эф(y)

                                   F_эф(y₂)

                                   F_эф(y₄)

F_эф(y₃)

F_эф(y₁)

                                                                                           y

                                                    y₁    y₃    y₄     y₂              

Рис. 5.8. Функция распределения эффективных электронов у катода растает до пробоя промежутка. Требуется определить закон распределения пробивных напряжений F_пр(U). Допустим, что промежуток обладает такой конфигурацией электрического поля, при которой на интервале значений (y₁, y₂) выполнение условия самостоятельности разряда приводит к пробою промежутка, т. е. начальное напряжение равно пробивному

U₀(y) = U_пр(y)                                   (5.38)

Рассчитаем с помощью (5.31) зависимость U0(y) и отметим на ней диапазон изменения y, на котором выполняется условие (5.38). Эта зависимость приведена на рис. 5.9.

Дальнейшее решение связано с вычислением закона распределения функции случайной величины U_пр(y) по известному закону распреде

56

сии. Причем для удобства вычислений целесообразно по ис ходному статистическому ряду образовать сгруппированный ряд слу чайных величин Х = tgd %. Данные сведены в табл. 5.4.

Выборочный момент помечен тильдой для сгруппированного ряда 6,0%, а выборочная дисперсия - 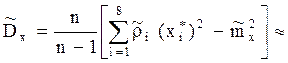 4,6 %. Равномерное распределение по (5.1) окажется

                                           ì 

f(x) = í

î     0,         x < a  или  x > b

и зависит от двух параметров a и b. Эти параметры следует выбирать так, чтобы теоретические моменты  и  равнялись соответствующим выборочным моментам и  . Разрешая два полученных уравнения относительно a b, имеем a » 2,3, b » 9,7. Гистограмма f(x) и выравнивающий ее равномерный закон f(x) =  показаны на рис.5.7. 

f(x)                

f(x)

0,1

x

2        4        6          8       10  %

Рис. 5.7. Функции распределения значений диэлектрических потерь

41