Координация изоляции электрооборудования: Учебное пособие к практическим занятиям, страница 21

Нормирующий множитель  необходим для выполнения условия нормировки 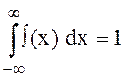, откуда, используя выражение            Р(a £ Х < b) = F(b) – F(a) и (5.7), получаем                                                                            А =

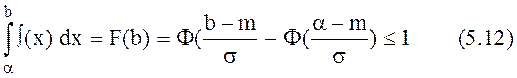
29

чайных величин. Измерения, выполненные на линиях  электропередачи (ЛЭП), подстанциях, исследовательских стендах и т.п. показали, что амплитуда и крутизна тока молнии изменяются в широких пределах, а их безусловные функции распределения могут быть представлены в виде экспоненциальных законов распределения

                          P(I > I_м) = ,                    (6.1)

                       P(a > a_м) = (a_м) = exp(- k_a a_м),                    (6.2)

где I_м и a_м выражаются в кА и кА/мкс, для равнинных районов до 500 м над уровнем моря k_I » 1/26 кА-1, k_a » 1/15,6 мкс/кА, а для горных районов выше 700 м над уровнем моря величина этих коэффициентов  уменьшается вдвое.

Так в первом приближении считают, что эти характеристики являются независимыми случайными величинами, то для них справедливо

P(I > I_м, a > a_м) = P(I > I_м) P(a > a_м) или (I_м,a_м) =

= exp[-(k_I I_м + k_a a_м)].                        (6.3)

Например, для разряда молнии в воздушные ЛЭП может быть приведен экспериментальный вариационный ряд значений тока молнии по табл. 6.1.

Таблица 6.1

Дискретные значения тока молнии на ЛЭП в кА

Cтатистические вероятности _мах, рассчитанны по ,

67

Моменты усеченного распределения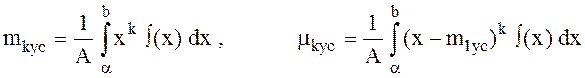     

выражаются через моменты m_k, m_k нормального распределения. Так, например, среднее значение момента m_k равно где 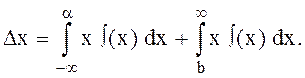 В случае когда  и  больше двух, моменты усеченного нормального закона приближенно равны соответствующим моментам нормального закона. Заметим, что “усекать” можно любой другой закон распределения случайных величин.

Нормальный закон распределения величин имеет вид по рис.5.1.

                                            f(x)

0                   m                 x

Рис. 5.1. Нормальный закон распределения случайных величин

ЛОГАРИФМИЧЕСКИ-НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. Положительная случайная величина Х имеет логарифмически-нормальное (логнормальное) распределение, если ее логарифм Y = s lnХ распределен по нормальному закону с дисперсией s² = и математическим

30

ЗАДАНИЕ 6.ВЕРОЯТНОСТНЫЕ ЗАДАЧИ

ПО ПЕРЕНАПРЯЖЕНИЯМ

6.1. ОЦЕНКА ПРЯМОГО УДАРА МОЛНИИ.

            Электрический разряд в виде молнии является источником грозовых (внешних) перенапряжений в электроустановках. В результате разряда молнии непосредственно в токоведущий участок конструкции электроустановки либо вблизи нее к изоляции прикладывается импульсное напряжение, которое может достигать больших и опасных для этой изоляции величин. В первом случае перенапряжение называют при прямом ударе молнии (ПУМ), а во втором – индуктированным.        Молния – это искровой разряд в длинном промежутке между облаком и землей, когда по одному и тому же каналу разряда протекает несколько импульсов тока с различной амплитудой и длительностью. Кривая импульса тока i_м может быть изображена в виде импульса с косоугольным фронтом и постоянной амплитудой по рис. 6.1.

i_м

I_м

a_мt

t

t_ф

Рис. 6.1 Форма импульса разряда молнии

Скорость нарастания импульса до амплитудного значения называется крутизной тока молнии a_м,а время нарастания t_ф = I_м / a_м - длительностью фронта. Амплитуда и крутизна тока молнии зависят от большого числа различных факторов и образуют систему двух слу

66

ожиданием

o = , где a = , а плотность распределения f(x) = 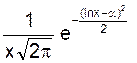. Логнормальная величина Х – безразмерная. Переход к размерной величине Х1 = n Х осуществляется умножением на масштабный множитель n.