5.1. Источники построения мат моделей
Каким образом получают математические модели ? Получение мат моделей – это искусство
Принципиально выделяются два пути построения мат моделей:
- на основе использования законов предметной области
- на основе экспериментов.
В первом случае мат модели формируются на основе использования законов, справедливых в рамках определенной предметной области (фундаментальных законов различных наук).
Типичным примером является использование физических законов при составлении д.у. маятника или колебательного контура. Однако часто законы неизвестны или они не выражаются количественно.
Во втором случае законы неизвестны. Данные для модели системы получают на основе экспериментов.
Характерно при этом, что принимаются некоторые предварительные гипотезы о характере зависимостей между переменными, описывающими систему.
Типичной ситуацией является рассмотрение выходной величины системы как линейной функции некоторых экзогенных переменных.
В связи с этим необходимо упомянуть о наличии развитой математической дисциплины – теории планирования эксперимента. Такая дисциплина позволяет получить максимум информации для построения математической модели системы при минимуме проведения экспериментов.
М. методы теории планирования эксперимента основаны на кибернетическом представлении процесса проведения эксперимента. Наиболее подходящей моделью последнего является абстрактная модель, называемая “черным ящиком”.
Под экспериментом понимается целенаправленно проводимый опыт, содержащий наблюдения исследуемого явления в специально создаваемых условиях, позволяющих следить за ходом явления с необходимой точностью.
Различные эксперименты: 1)Лабораторные, поставленные в спец. условиях; 2)Производственные; 3)Натурные; 4) На ЭВМ.
При таком кибернетическом подходе различают входные и выходные переменные. Входные переменные обычно называются факторами, а выходные переменные – реакцией. В зависимости от того, сколько в эксперименте рассматривается факторов, они называются одно-, двух- и более факторными экспериментами. Эксперимент должен планироваться. Основная цель этого состояния в том, чтобы получить максимум информации об объекте при минимуме затрат на проведение эксперимента.
В условиях проектирования чаще всего имеется некоторый арсенал опробованным математических моделей, использующихся при анализе эффективности проектируемых систем.
5.2. Требования, предъявляемые к математическим моделям
Основные требования, предъявляемые к моделям:
- точность (адекватность);
- универсальность;
- экономичность.
Точность м.м. определяется как степень
совпадения предсказанных с помощью этой модели значений параметров объектов
(эта характеристика определяется также как степень совпадения выходных параметров
модели и объекта).
Пусть Yi – это выходной параметр моделируемой системы, а Yi – это тот же выходной параметр, рассчитанный с помощью
модели. Тогда в качестве оценки точности модели может быть использована
относительная погрешность модели по i-му выходному параметру.
ei= (Yi-Yi)/Yi
Если система имеет вектор Y с m компонентами, то для оценки точности модели можно использовать выражения вида:
e =мах l ei
l i=1,m
e =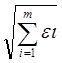
На практике оценка точности, по выше приведенным формулам, встречает определенные трудности в большинстве случаев, точные решения Y оказываются неизвестными.
Степень точности м.м-ей определяется их применимостью и анализ более или менее многочисленной группы однотипных объектов.
Желательно, чтобы инженер-разработчик был освобожден от сложной и ответственной работы по конструированию м. м-ей и прибегать к ней только в исключительных случаях.
Поэтому применяемые в САПР модели должны иметь более высокую степень универсальности.
Экономичность модели оценивается затратами машинного времени на моделирование. (В настоящее время этот критерий малоактуален).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.