В рамках рассматриваемой математической схемы предполагается, что переход системы из одного состояния в другое возможен только в строго определенные, заранее фиксированные моменты времени: t1, t2, t3, … В промежутках времени между этими моментами система сохраняет свое состояние. (Считается, что в момент t0 система находится в некотором исходном состоянии z0 ). Будем называть указанные моменты времени шагами или этапами процесса.
Случайный процесс, происходящий в системе, состоит в том, что в последовательные моменты времени t1, t2, t3, … система оказывается в тех или других состояниях, ведя себя, например, следующим образом:
z0 ® z1 ® z3 ® z2 ® z3 ® z0 .
Пример такого поведения системы иллюстрируется рисунком 4.3.
В общем случае система в моменты t1, t2, t3, … может не только менять состояния, но и оставаться в прежнем состоянии.
Условимся обозначать символом Si(k) случайное событие, состоящее в том, что после k шагов система находится в состоянии zi . (Исходное состояние системы соответствует нулевому шагу).
Процесс, происходящий в системе, можно представить как последовательность (цепь) событий, например,
S0(0) , S1(1), S3(2), S2 (3), S1 (4) , …
Такая случайная последовательность событий называется марковской цепью если для любого шага вероятность перехода из любого состояния в любое другое состояние не зависит от того, когда и как система пришла в это состояние.
Будем описывать марковскую цепь с помощью так называемых вероятностей состояний. Такие вероятности оценивают возможности свершения событий Si(k) (оценивают возможность нахождения системы в определенном состоянии на определенном шаге). Для их обозначения используется следующая символика:
pi(k) = P( Si(k) )
Так, например, вероятности нахождения системы во всех ее возможных n состояниях после первого шага описываются следующим набором:
p0 (1) = P( S0 (1)), p1(1) = P( S1(1)), p2(1) = P( S2(1)) , …. , pn-1(1) = P( Si-1(1)) .
Основной задачей моделирования дискретной марковской цепи является определение вероятностей состояний системы pi(k) для любого k (вероятностей нахождения системы в том или ином состоянии на определенном шаге).
Изобразим состояния системы в виде графа (рис. 4.4), где стрелками указаны возможные переходы системы из состояния в состояние за один шаг.
Случайный процесс (марковскую цепь) можно представить себе так, будто точка, изображающая систему, случайным образом перемещается (блуждает) по графу состояний, перескакивая из состояние в состояние в моменты t1, t2, t3, …, а иногда и задерживаясь в том же состоянии.
Рис. 4.4
Для любого шага (момента времени t1, t2, t3, … ) существуют некоторые вероятности перехода системы из любого состояния в любое другое (некоторые из таких вероятностей могут быть равны нулю). Будем называть эти вероятности переходными вероятностями марковской цепи.
Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага. В противном случае марковская цепь называется неоднородной.
Однородная марковская цепь может быть задана с помощью матрицы переходных вероятностей. Для системы, имеющей n состояний z0 , z1 , z2 , …, zn-1 такая матрица будет иметь следующий вид
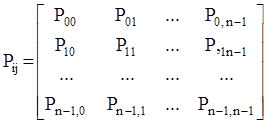(4.16)
Элемент такой матрицы Pij – вероятность перехода системы из состояния i в состояниеj за один шаг (i, j =1,2,…,n-1).
Переходные вероятности удобно изображать на графе сети, проставляя значения вероятностей над соответствующими дугами. (Полученный таким образом граф называется размеченным графом состояний).
Имея матрицу переходных вероятностей (или размеченный граф состояний) и зная начальное состояние системы z0 , можно последовательно найти вероятности состояний p0(k), p1(k), p2(k),…,pn-1(k) после любого (k-го) шага [ ].
При этом используется следующая рекуррентная формула
pi(k) = 
(i
=0,1,…,n-1) (4.17)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.