Моделирование систем: Учебное пособие (Структуры функциональных математических моделей систем. Общие вопросы математического моделирования систем), страница 12

3.3  Аналитические, аналитико-алгоритмические  и  алгоритмические модели

Данная классификация характеризует характер связей независимых переменных модели с зависимыми переменными

Аналитические модели  имеют форму явных зависимостей зависимых переменных модели от независимых переменных. К такому классу относятся модели вида (2.1) и (2.6), а также композиции отображений вида (2.2) и  (2.3)

Подчеркнем, что такие модели являются наиболее удобными для моделирования систем. При их использовании моделирование систем состоит в вычислениях значений зависимых переменных по заданным значениям независимых переменных по некоторой формуле (принцип “подставил – получил”). Кроме того, в этом случае есть возможность исследования  системы средствами математического анализа в общем  виде.

З а м е ч а н и е 3.3. Исследование в общем виде состоит в исследовании зависимостей на уровне переменных модели. При таких исследованиях не определяются какие-либо численные значения переменных.

Аналитико-алгоритмические модели представляют собой различного рода уравнения (дифференциальные, интегральные, алгебраические и др.) или системы уравнений, связывающие независимые и зависимые переменные модели.

Первоначально такая модель записывается в аналитической форме, в виде некоторых формул, с использованием символов функций и специальных операторов (например, дифференциальных). Однако непосредственно произвести расчет зависимых переменных модели по заданным значениям независимых по такой модели невозможно.

Для этого необходимо осуществить процедуру решения уравнения, представляющую собой некоторый алгоритм.

В результате такого решения могут быть получены явные зависимости зависимых переменных модели от независимых переменных в виде некоторых формул. Вместе с тем, имеют место случаи, когда осуществить такое решение оказывается невозможным (невозможно, например,  получить аналитическое решение дифференциального уравнения).

К моделям такого вида относятся модели (2.7), (2.8). К необходимости решения уравнений для осуществления моделирования приводит и использование аналогов моделей видов (2.1) и (2.2), имеющих неявную форму.

Очевидно, что такие модели являются менее удобными для моделирования, чем аналитические модели.

Алгоритмические модели  представляют собой некоторые алгоритмы, выполнение которых позволяет определить значения зависимых переменных модели по заданным значениям независимых переменных.

Такие модели обычно являются более громоздкими, чем аналитические. Кроме того, они не позволяют произвести анализ системы в общем виде.

4. Типовые математические схемы

4.1. Общие положения

Понятие “математическая схема” характеризует один из этапов построения математической модели системы. Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы  (с учетом внешней среды) [3].

Процесс моделирования системы обычно представляет собой последовательность следующих этапов: “объект моделирования - концептуальная модель – математическая схема – математическая модель” (рис. 4.1).

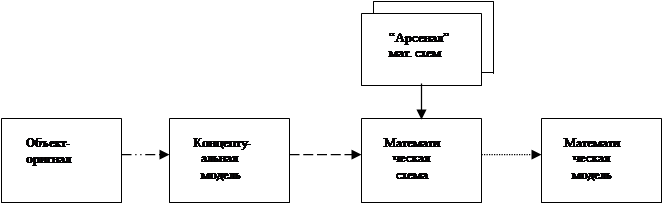Рис. 4.1

На начальном этапе моделирования  у человека формируется концептуальная модель объекта. Такая модель содержит представления  человека об объекте. Обычно такая модель может быть сформулирована  в словесной форме.

Математическая схема предоставляет в распоряжение человека некоторый набор достаточно абстрактных понятий  и представлений, в рамках которых может быть описана система на базе ее концептуальной модели. Задача человека состоит в “переводе” его представлений в представления, предусмотренные математической схемой. Можно сказать, что математическая схема “предлагает” некоторый набор абстрактных понятий. При использовании такой схемы осуществляется интерпретация компонентов моделируемой системы в рамках этих понятий.