Геофизические методы исследований. Обработка результатов полевых гравиметрических измерений. Количественная интерпретация кривых ВЭЗ, страница 22

В зависимости от типа регистрируемых сейсмических волн, образующихся при наличии одной границы раздела упругих свойств различают годографы прямой, отраженной и преломленной волн.

Линейный продольный годограф прямой волны описывается уравнением 

x t =±

v

и состоит из двух отрезков прямых (рис. 11), исходящих из начала координат (принято, что источник помещен в начало координат) под углом ψ. Эти отрезки называют ветвями годографа - правой и левой. Наклон ветвей определяется только скоростью и связан с нею простым соотношением

                                                                    Δt        1

                                                      tgψ =        =

                                                                    Δx        v₁

                                                                              .

Следовательно, по наклону годографа прямой волны можно определить скорость распространения сейсмических волн.

62 над центром шара

GM Δg max =         2 h

, так как х в этой точке равно нулю. Следовательно эта точка является началом координат. 

Для определения глубины залегания центра шара h на оси абсцисс возьмем точку x_n в которой значение поля равно Δg_n   и  найдем отношение

                                       Δg                           1

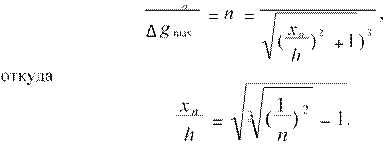
В частности для точки, удаленной от максимума на расстояние x_0.5, мы будем иметь 

xⁿ

                                         = 0,77 ,

                                         h

отсюда находим глубину залегания центра сферы h 

h =1.3x_0.5

.

Избыточную массу находят по формуле 

M =Δgmaxh2 /G

Величины х₀,₅ и Δg _max снимают с графика (см. рис. 2.)

Если известна избыточная плотность δсферического тела, то можно определить его объем и радиус R из соотношения

M =Vδ=πR³δ

Тогда глубина до верхней кромки будет h₁= h-R, а до нижней поверхности сферы h₂ =h + R.

Решение прямой задачи для тела в виде горизонтального кругового цилиндра имеет вид _2Gλh

            Δg = 2 2             x +h

где G - гравитационная постоянная; ; h - глубина залегания центра сферы; х - абсцисса произвольной точки на оси х, λ - линейная плотность цилиндра (λ=πR² δ).

Кривая всюду положительна и симметрична относительно максимума который находится над центром горизонтального цилиндра. Следовательно начало координат совпадает с максимумом кривой т.е.при x=0.

        _Δg max ₌ 2G^λ _.               Рисунок 3. Гравитационное поле

                               h                    над бесконечным горизонтальным

Для определения глубины залегания центра цилиндра используем соотношение

                                   Δg_n                                                  1

 

отсюда 

В частности для точки, удаленной от максимума на расстояние x_0.5, мы будем иметь 

x0,5=h.

Если известна избыточная плотность то можно найти радиус цилиндра

 

                                                 R =.

Аналитические формулы разработаны для различных тел. Для тел более сложной формы уравнения будут сложнее, а форма

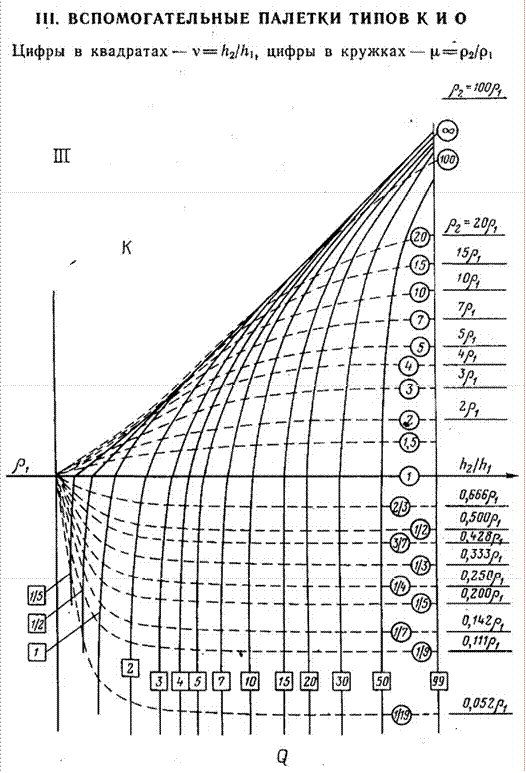
Рисунок 10. Вид вспомогательных палеток типов K и Q

61

графиков и распределение аномалий по площади различны, но во всех случаях могут быть установлены элементы залегания тел по аномалиям ускорения свободного падения или градиентам гравитационного поля.

Лабораторная работа  «Количественная интерпретация гравитационных аномалий»

Материалы и оборудование: калькулятор, график аномально      го поля полученный в предыдущей лабораторной работе. Цель работы: приобретение навыков количественной интерпретации данных гравиразведки.

Задание

Провести количественную интерпретацию гравитационной аномалии полученной в ходе выполнения предыдущей лабораторной работы. При интерпретации учитывать что четные варианты соответствуют  аномалии от шара а нечетные от горизонтального кругового цилиндра. Расстояние между пикетами Δх и значение избыточной плотности δ дано в табл. 2.  

.