Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа

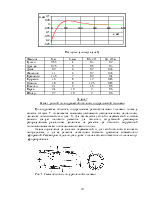
Задача 5

Расчёт конической оболочки

а) случай распределённой нагрузки

Коническая оболочка с углом α при вершине нагружена нормальной к поверхности равномерно распределённой нагрузкой q, как показано на рисунке (а). Закрепления во внимание не принимаем. Требуется рассчитать усилия в оболочке.

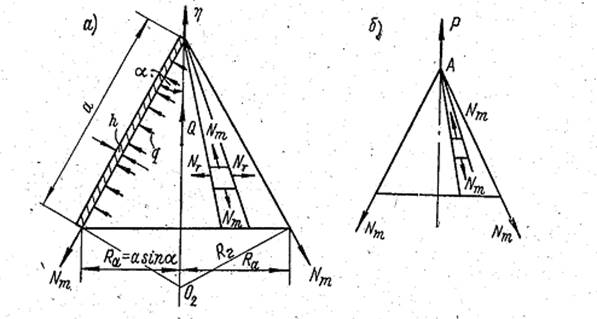
Для рассматриваемой оболочки главные радиусы кривизны

R₁=∞ и R₂=a·tgα, и из уравнения Лапласа 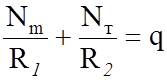 находим

.

Из уравнения равновесия

Q - N_m·2πRa cos α = 0, где Q — равнодействующая проекций на ось η нормальных давлений на оболочку.

Так как при длине образующей а боковая поверхность оболочки

S = πR_aa = πа² sinα, равнодействующая Q получается равной

Q = qSsin a = qπa²sin²α.

Меридиональное усилие

.

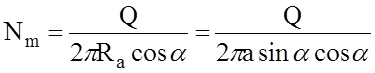Если в это выражение подставить найденное значение Q, то

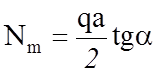
и

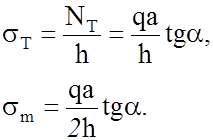
Зададим для определённости исходные данные. Пусть a = 30⁰, а = 2 м и q = 500 кПа (что соответствует давлению столба воды в 50 м). Предполагая, что материал конуса – обычная углеродистая конструкционная сталь с пределом текучести s_т = 235 МПа и принимая коэффициент запаса прочности по пределу текучести равным 2,0, рассчитаем минимально допустимую толщину конуса по условию прочности. Расчёт выполним по приведённым напряжениям, которые примем равными

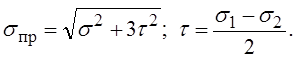
Вершина конуса является особой точкой, вблизи которой появляются изгибные напряжения, которыми мы пренебрегаем. После подстановок получаем следующие результаты:

- тангенциальное усилие (вдоль окружности) N_т = 577 кН/м;

- меридиональное усилие (вдоль образующей) N_m = 289 кН/м.

Эти усилия подсчитываются на единицу длины соответствующей линии. Они не зависят от расстояния сечения от вершины конуса – по мере удаления от неё растёт нагрузка на кольцевое сечение, но пропорционально растёт и длина сечения.

Установим соотношение между наибольшими (тангенциальными) s₁ и приведёнными s_пр напряжениями. Прежде выясним, какова величина касательных напряжений.

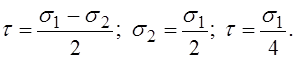
Тогда

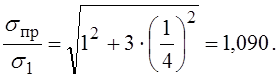
Этот множитель можно ввести, например, в коэффициент запаса. Тогда допускаемые тангенциальные напряжения составят 235 / 2 / 1,090 = 108 МПа.

Площадь на единицу длины сечения, очевидно, равна толщине конуса h. Зная действующее усилие N_т = 577 кН/м и допускаемое напряжение [s] = 108 МПа, находим требуемую толщину, разделив первое на второе. При этом важно учесть, во-первых, несовпадение размерностей обеих величин, во-вторых, желательность получить толщину не в метрах, а в миллиметрах. Для согласования размерностей результат нужно умножить на 1000, для перевода толщины из метров в миллиметры, наоборот, разделить на 1000. Значит, множитель для получения нужного результата равен 1:

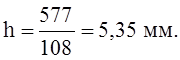
Выражение для меридионального усилия N_m справедливо также в случае сосредоточенной силы Р,приложенной к вершине А конической оболочки по её оси (рисунок 1, б). Равнодействующую Q в формуле нужно в этом случае заменить на Р. Так как при этом распределённое давление q равно нулю, из уравнения Лапласа следует, что окружное усилие N_T и окружное напряжение σ_Т равны нулю. Но величина меридионального напряжения при этом будет переменной вдоль образующей.

б) случай сосредоточенной силы

Пусть теперь сосредоточенная сила Р приложена к вершине конической оболочки и направлена по нормали к оси конуса (рисунок 2, а). Вырезанный из оболочки двумя горизонтальными сечениями и двумя образующими элемент находится в равновесии. Для нахождения меридиональных усилий N_m условие равновесия составляется путём приравнивания нулю суммы проекций сил, приложенных к элементу, на ось Т, направленную по образующей конуса (рис. 2, а и б).

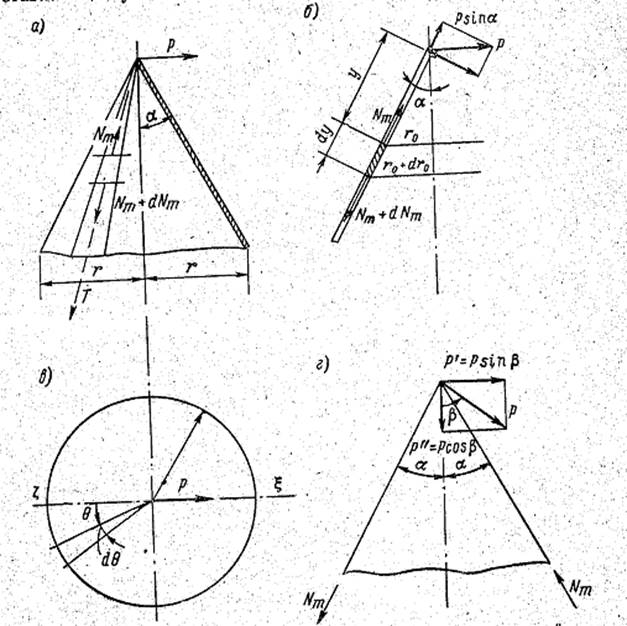
Рис. 2. Коническая оболочка, нагруженная силой, действующей под углом к оси вращения

Радиусы кривизны верхней и нижней граней элемента

Поэтому сумма проекций на ось Т

После раскрытия скобок, сокращения и отбрасывания слагаемого высшего порядка малости уравнение примет вид

или

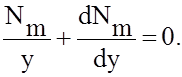
Это уравнение удовлетворяется выражением

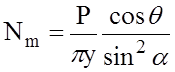, которое можно получить, проектируя силу Р и силы N_m, приложенные к оболочке, на образующую, лежащую в плоскости, составляющей угол θ с плоскостью действия силы Р.

Сумма моментов сил N_m относительно оси ζ – ξ, образующей угол θ = π/2 с плоскостью действия силы Р (рис. 2, б), равна P×y×cosα, т.е. моменту силы Р относительно этой оси.

Экваториальные погонные усилия N_T получаются из уравнения Лапласа при ρ₁ = ∞ равными нулю.

Если сосредоточенная сила Р приложена к вершине конической оболочки в направлении образующей конуса (рис. 2, в), её можно разложить на составляющие:

— по направлению оси конуса

Р'= Р cos α;

— горизонтальную

Р" = Р sin α.

Использовав формулы, приведённые выше, получим меридиональное усилие в этом случае

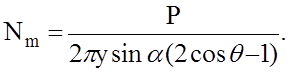
Если сосредоточенная сила Р приложена к вершине конической оболочки под произвольным углом β к оси вращения η оболочки (рис. 2, г), то она может быть разложена на составляющие Р' и Р", действующие соответственно по оси вращения и по образующей (или по оси вращения и перпендикулярно к ней). Усилия N_m и N_T,. возникающие в оболочке от произвольной cилы Р, могут быть найдены в виде алгебраической суммы усилий, вызванных составляющими Р' и Р".