Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 23

Чтобы устранить этот разрыв, необходимо приложить моменты М₀. Так как соответствующее частному решению (10) напряжение s_j компенсирует напряжения (7), то мы заключаем, что напряжения, вызванные моментами М₀, представляют собой полные температурные напряжения, вызванные указанным выше падением температуры. Если расстояния поперечного сечения mn от концов цилиндра велики, то значение момента М₀ можно получить путём подстановки

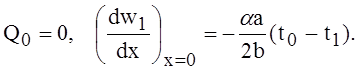
непосредственно из уравнения

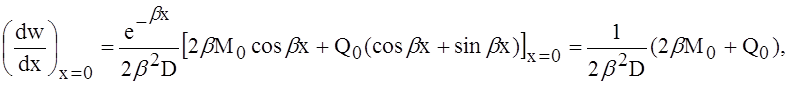которое даёт

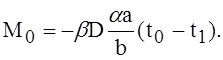                                                                                     (12)

Внеся сюда вместо b его значение из соответствующего выражения и взяв n = 0,3, найдём, что максимальное температурное напряжение равно

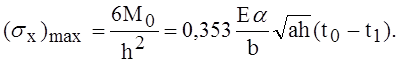                                                  (13)

В этих подсчётах предполагалось, что расстояние bдо торца цилиндра велико. Если в действительности это не так, то в значение момента (12) должна быть внесена поправка, вычисление которой производится следующим образом. В бесконечно длинной оболочке момент М₀ вызывает на расстоянии х = b появление момента и перерезывающей силы (рисунок с), определяемых общим решением:

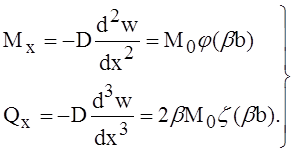                                                                       (14)

Здесь использованы обозначения функций:

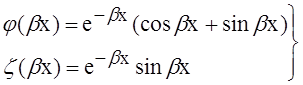
Так как на расстоянии х = bу нас имеется свободный край, то для устранения сил (рисунок b) нам необходимо приложить момент и силу, величины которых равны

                                                (15)

Момент, произведённый силами (15) в поперечном сечении (mn), даёт искомую поправку , которую нужно внести в значение момента (12). Величина этой поправки определяется уравнением

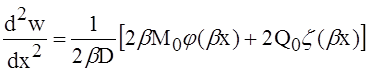, если вместо М₀ мы подставим в него  вместо Q. Эти подстановки дают

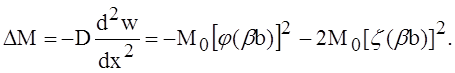                                    (16)

Рассмотрим для примера чугунный цилиндр следующих размеров: а = 246 мм, h = 35 мм, b = 108 мм, a = 101 10 ^-7, Е = 9,1 × 10⁶ кг/см², t₀ - t₁ = 180° С. Тогда формула (13) даёт

s_mах = 656 кг/см².

Вычисляя поправку (16), имеем

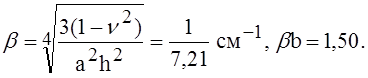
Тогда

Отсюда по формуле (16)

DM = -М₀ (0,238² + 2 × 0,223²) = -0,156М₀.

Это указывает на то, что для получения истинного максимального значения температурного напряжения вычисленное выше максимальное напряжение нужно уменьшить на 15,6 %.

Исходные данные (задача 13)

Фамилия	a, мм	h, мм	b, мм	Dt, град.
Гунько	150	8	200	100
Дроздов	165	8	200	100
Дюба	180	8	200	100
Железнов	200	8	200	100
Кравченко	220	8	200	100
Купресов	240	8	200	100
Останин	260	8	200	100
Потенко	280	8	200	100
Царёв	300	8	200	100
Шкляр	330	8	200	100

Материал – сталь, Е = 2,05·10⁵ МПа, a = 1,2·10^-5.

Задача 14а

Ребро в виде короткой цилиндрической оболочки

Круглая пластина, подкреплённая высоким кольцевым ребром, нагружена, как показано на рисунке а. Дано: а = 16 см; b = 10 см; с = 24 см; h = 1,0 см; h₁ = 1,6 см; l = 2,8 см; H = 2 см; Р = 1000 Н/см.

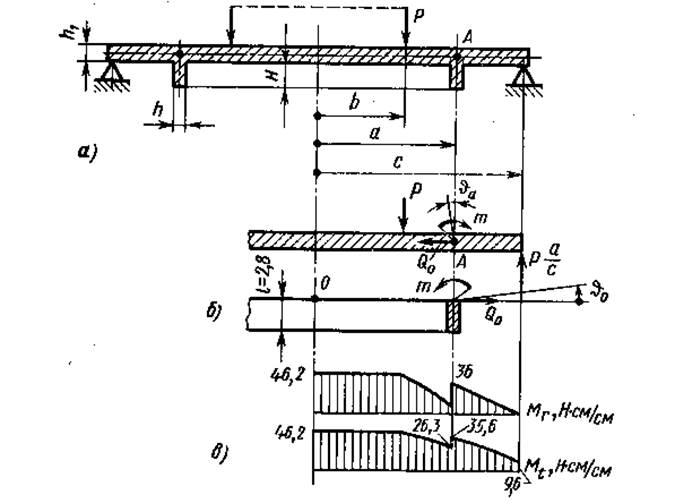
Поскольку в данном случае высота ребра значительна, то его следует рассматривать как короткую цилиндрическую оболочку.

Отделим ребро от пластинки. За точку сопряжения примем точку пересечения срединных поверхностей. При таком способе разделения некоторая часть объёма оказывается учтённой дважды, так как она относится и к пластине, и к ребру. Это приводит к некоторой погрешности, однако вследствие малости упомянутого объёма, а также малой его напряжённости (объём расположен близко от срединной поверхности пластины) эта ошибка невелика. Вместе с тем при таком способе разделения вычисления значительно упрощаются. Заметим, что другой способ разделения (по плоскости, совпадающей с нижней плоскостью пластины) также не свободен от погрешности, так как в области сопряжения гипотеза неискривляемости нормали точно не соблюдается. При решении примем допущение, что деформация растяжения срединной плоскости равна нулю.