Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 20

Считаем, что на оболочку действует поверхностная распределённая нагрузка, которую можно представить в виде суммы трёх составляющих:

р₁ – по нормали к поверхности; р₂ – по касательной к меридиану; р₃ – по касательной к параллели.

Ветровой называется поверхностная нагрузка вида

 

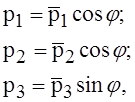
где  — функции, зависящие только от q.

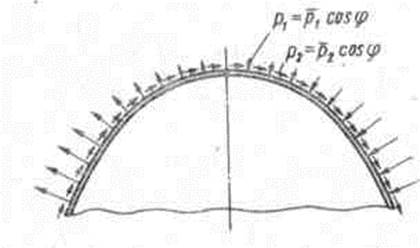
Эта нагрузка представляет собой наиболее простой частный случай несимметричной поверхностной нагрузки. Некоторое представление о характере ветровой нагрузки даёт рисунок, где показана оболочка в разрезе с действующими на неё нагрузками р₁ и р₂ (функция  в данном случае — отрицательная). Вместо обычных в подобных задачах рядов в данном случае имеется только по одному слагаемому, соответствующему k = 1.

Используется дифференциальное уравнение вида

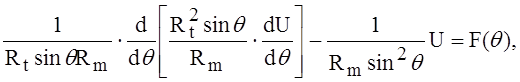                                                                                                              (1)

где F (q)—функция поверхностной нагрузки;

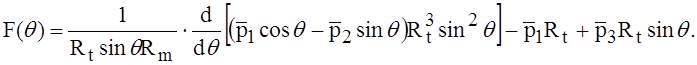            (2)

Здесь R_m - радиус кривизны меридиана; R_t - радиус кривизны в направлении, перпендикулярном меридиану. Они являются главными радиусами кривизны. Угол j отсчитывается от некоторого нулевого меридиана, угол q - между осью вращения и нормалью к поверхности оболочки.

Функция U (в общем случае произвольной нагрузки – U_k(q)) определяется выражением

где, если опустить подробности, с помощью слагаемых  получается T_m - нормальная сила в меридиональном направлении (по касательной). Силу, действующую по касательной к параллели, обозначим T_t, а сдвигающую силу - S. Связь этих сил с действующими напряжениями устанавливается формулами:

Введём новую переменную

                                                                                            (3)

Тогда

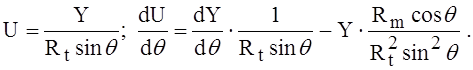
Здесь учтено, что

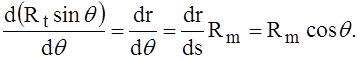
После замены переменной дифференциальное уравнение принимает вид

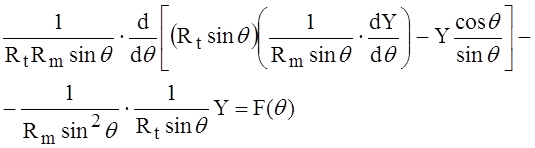
или после простых преобразований

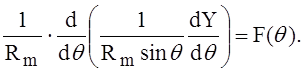                                                                     (4)

Интегрирование этого уравнения не вызывает затруднений. После первого интегрирования

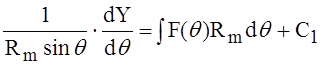
и после второго интегрирования

                               (5)

Предположим, что оболочка имеет сферическую форму (R_m = R_t = R) и что составляющие нагрузки р₂ и р₃ равны нулю, а составляющая р₁ определяется равенством

В этом случае функция F (q) (см. равенство (2)) принимает вид

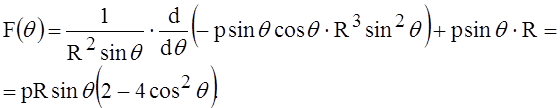
Подставим F (q) под знак интеграла и выполним интегрирование:

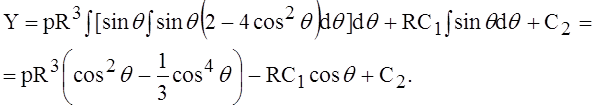            (6)

Вычислим ещё производную функции Y:

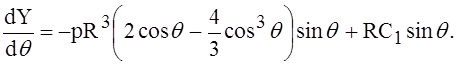                                       (7)

Для определения постоянных C₁ и С₂ используем условия симметрии относительно плоскости j = 0 и обратной симметрии относительно плоскости j = 90°. На основании этих условий при q = 0 должно обращаться в нуль как меридиональное усилие , так и сдвигающее усилие .

Согласно ранее полученным равенствам, можно записать

                                                                                                (8)

Но при q = 0,  = 0 и, кроме того, sinq = 0, следовательно, Y(0) = 0, откуда с учётом равенства (6):

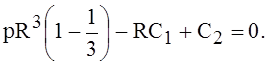                                                                            (9)

Чтобы получить второе уравнение с неизвестными С₁ и С₂, продифференцируем равенство (8) по q и разделим на sin q:

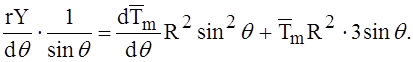                                               (10)

 

При q = 0 правая часть равенства (10), очевидно, обращается в нуль. С другой стороны, эта же величина может быть выражена через С₁ из уравнения (7):

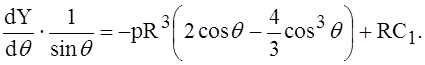
При q = 0

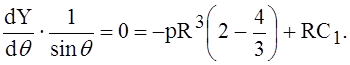
Отсюда

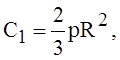
и тогда из уравнения (9)

С₂ = 0.

Выражения искомых функций имеют следующий вид:

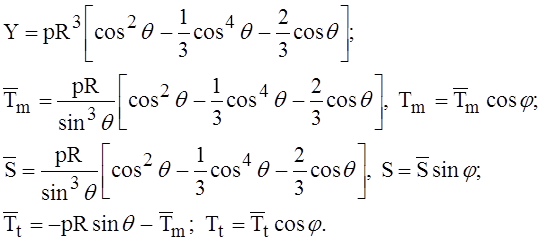
Эпюры внутренних усилий по углу q приведены на рисунке 1.

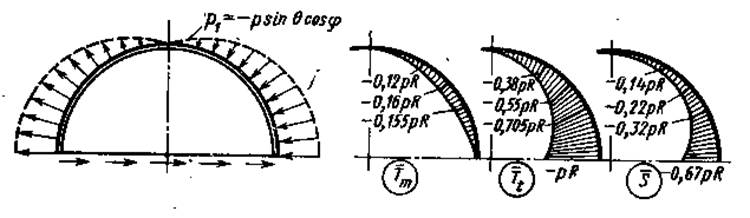
Рис. 1

Приведённое решение получено без учёта граничных условий на нижнем краю оболочки. Следовательно, оно будет справедливо в том случае, когда силы Т_m и S, приложенные к нижнему краю, будут распределены по закону Т_m =  cos j; S = sin j.