Второе граничное условие вытекает из рассмотрения взаимодействия оболочки и подкрепляющего её ребра жёсткости. Очевидно, что радиальные перемещения оболочки в опорных сечениях равны соответствующим радиальным перемещениям ребра жёсткости. Ребро жёсткости, которое будем называть шпангоутом, представляет круговое кольцо, нагруженное равномерным давлением (рис. 3).
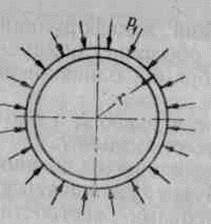
Рис. 3.
Интенсивность давления оболочки на шпангоут должна определяться, очевидно, удвоенной величиной перерезывающей силы в опорном сечении балки-полоски единичной ширины, выделенной из оболочки, т.е. должна быть равной
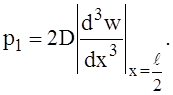 (4)
(4)
Величина напряжения, действующего в поперечном сечении шпангоута, будет определяться равенством
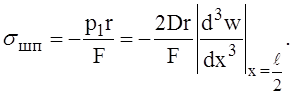 (5)
(5)
Так как шпангоут находится в условиях одноосного напряжённого состояния, его осевая деформация
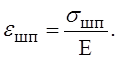 (6)
(6)
Осевая деформация шпангоута связана с его радиальным перемещением w зависимостью
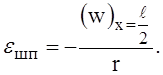 (7)
(7)
Сравнивая выражения (6) и (7) и принимая во внимание равенство (5), получим второе граничное условие для определения постоянных интегрирования в выражении (2)
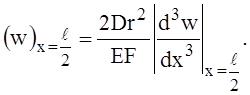 (8)
(8)
Подставляя выражение для w в граничные условия (3) и (8), получим два уравнения относительно неизвестных С1 и С2
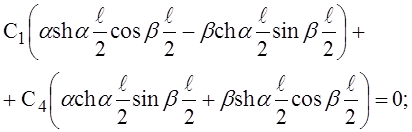
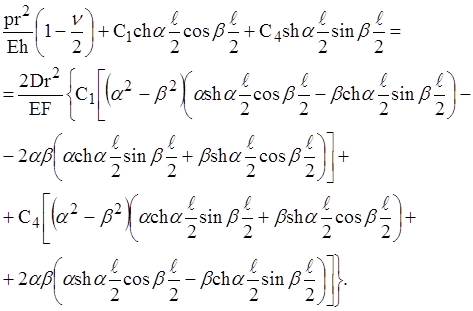
После несложных, но довольно громоздких преобразований найдём
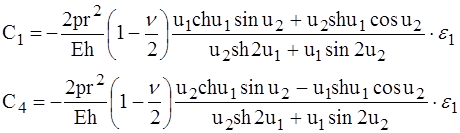 (9)
(9)
где
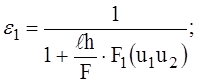 (10)
(10)
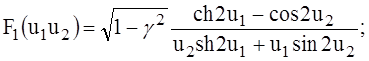 (11)
(11)
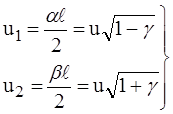 (12)
(12)
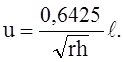 (13)
(13)
Подставляя значения постоянных Сi из равенств (9) в выражение (1), можно определить все интересующие нас элементы изгиба оболочки. Так, в частности, изгибающий момент М1 будет определён из выражения
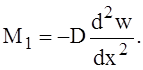 (14)
(14)
Так как наибольшие напряжения в оболочке могут возникнуть либо в её опорных сечениях на рёбрах жёсткости, где имеет место наибольший изгиб оболочки, либо в среднем её сечении между рёбрами жёсткости, где имеет место наибольшее обжатие оболочки (наибольшее радиальное перемещение w, рис. 4), для нас представляет интерес значение изгибающего момента в опорном сечении оболочки (х = 0,5l) и в середине пролёта (х = 0).
Подставляя значения Ci из уравнения (9) в выражения (1) и (14), получим
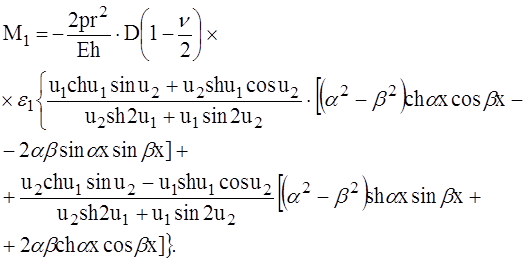 (15)
(15)
Интересующие нас значения моментов будут
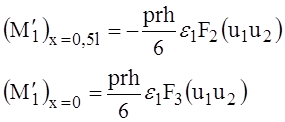 (16)
(16)
где
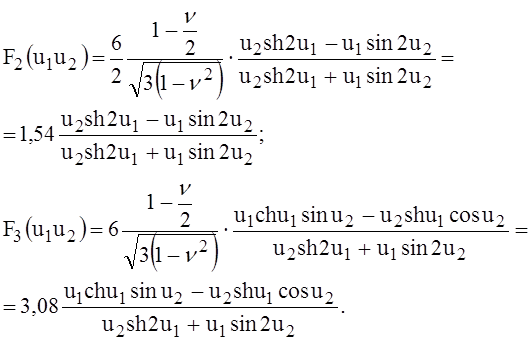 (17)
(17)
Нормальные напряжения в поперечных сечениях оболочки складываются из напряжений от сжатия оболочки вдоль оси, распределённых равномерно по её толщине, и напряжений от изгиба оболочки, меняющихся по её толщине по линейному закону.
Наибольшие нормальные напряжения будут на наружной и внутренней поверхности оболочки. Величина их может быть определена по формуле
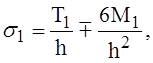 (18)
(18)
где верхний знак перед вторым членом правой части формулы (18) соответствует наружной поверхности оболочки, а нижний — внутренней,
Так как
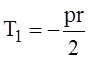
и М1 определяется выражениями (16), максимальное нормальное напряжение в поперечных сечениях оболочки будет: в опорных сечениях
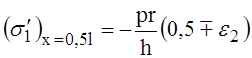
и в среднем сечении (19)
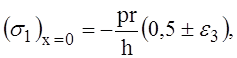
где
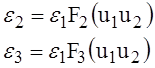 (20)
(20)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.