Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 24

В точке сопряжения А на ребро действуют момент m и поперечная сила Q₀ (рисунок б). Обозначим через q_а угол поворота нормали в точке сопряжения и через  - высоту ребра. Запишем граничные условия для ребра: при х = 0     w₀ = 0;       при х = 0    q₀ = q_а; при х = 0     Р₁ = Q₀;     при х = 0     М₁ = -m; при х = l      Р₂ = 0;       при х = l      М₂ = 0.

Применив зависимости, полученные для коротких цилиндрических оболочек, загруженных соответствующими нагрузками по кромкам, придём к двум уравнениям:

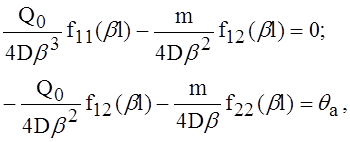
из которых найдём

 

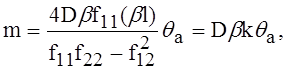
где

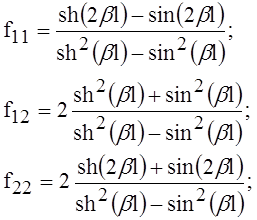
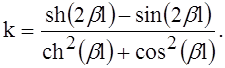
Принцип решения задачи базируется на методике расчёта круглых пластин с кольцевыми рёбрами. При переходе через сечение на радиусе установки ребра R_k условия сопряжения участков (постоянство углов поворота при наличии скачка моментов) можно записать в виде

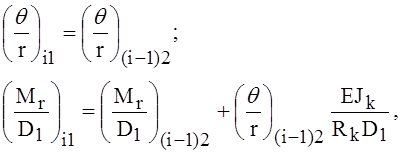
или в матричной форме

где L - матрица перехода через ребро.

Эта методика полностью применима и при расчёте пластин с высокими рёбрами. Матрица перехода через ребро будет иметь вид

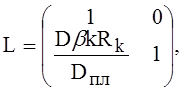
где D_пл — жёсткость первого участка пластины;

R_k — средний радиус окружности ребра.

В данном примере

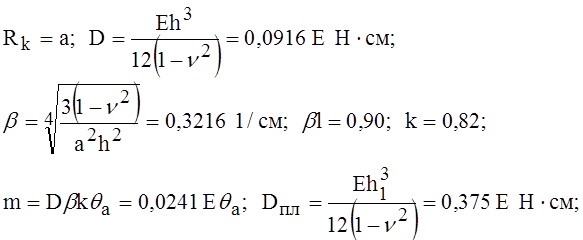
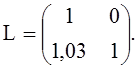
Для сравнения приведём результаты вычислений для ребра как кольца с недеформируемым поперечным сечением

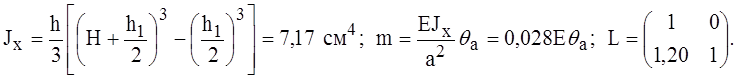            Разница в значениях податливости ребра в данном случае составляет 17%.

При  ребро допустимо рассматривать как кольцо с недеформируемым сечением; если же bl > 3, то ребро можно рассчитывать как длинную оболочку. При этом матрица L сохраняется без изменения, а параметр k будет равен 2.

Дальнейший расчёт пластины не приводим. Значения изгибающих моментов для данной пластины указаны на рисунке в.

Исходные данные (задача 14а)

Задача 14б

Ступенчатая крышка

Определить изгибающие моменты в ступенчатой крышке, изображённой на рисунке а. Крышка нагружена равномерным наружным давлением. Дано: а = 10 см; l = 3,1 см; h = 0,4 см.

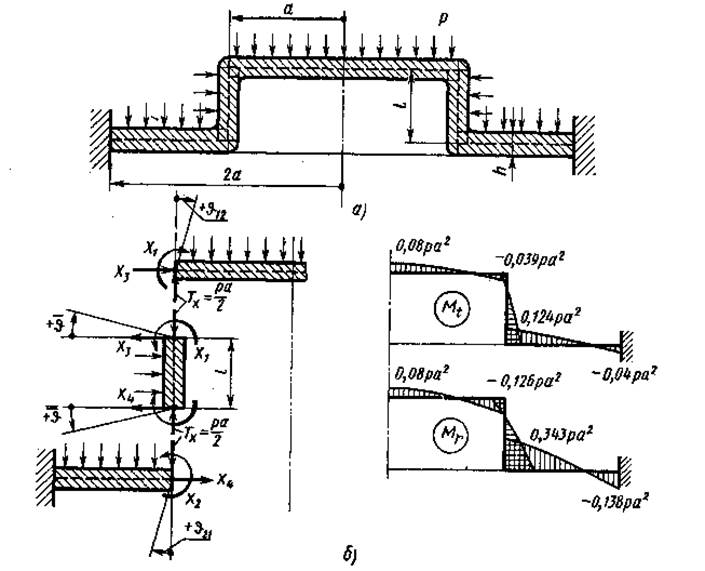
Заданную систему можно расчленить на две плоские пластины и короткую цилиндрическую оболочку (рисунок б). В местах сочленения действуют неизвестные силовые факторы Х₁, Х₂, Х₃, Х₄. Так как пластины имеют большую жёсткость на растяжение в своей плоскости, то можно считать, что радиальные перемещения w на краях цилиндрического участка равны нулю. Запишем условия сопряжения цилиндрического участка и пластин:

при х = 0 w = 0; q = q₁₂; при х = l w = 0; q = -q₂₁; где q₁₂ и q₂₁ — углы поворота нормалей на краях первой и второй пластины.

Положительные направления угловых перемещений указаны на рисунке б.

Угловые перемещения краев пластины вычислим по формулам, полученным для круглой пластины ступенчато-переменной толщины, подкреплённой кольцевыми рёбрами:

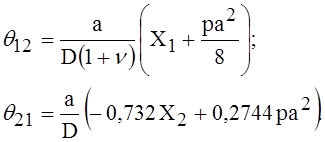
Перемещения краёв цилиндрического участка определим по соответствующим зависимостям с добавлением частного решения .

В результате подстановки значений перемещений условия сопряжения цилиндрического участка и пластин приводятся к системе четырёх уравнений:      

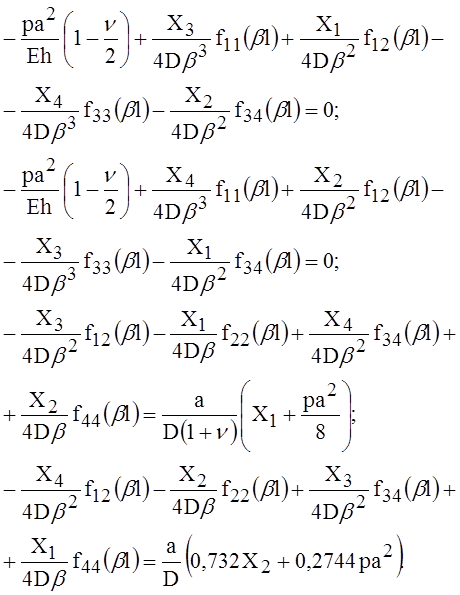
Здесь используются вспомогательные функции

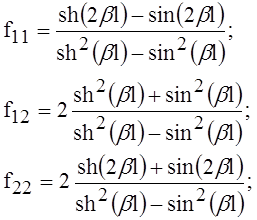
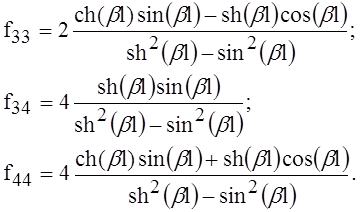
Параметр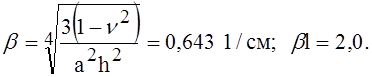

Значения функций влияния в нашем примере следующие:

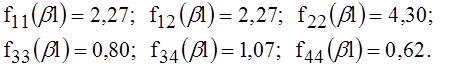
Подставив указанные величины в уравнения сопряжения и решив эту систему, получим значения силовых факторов:

Х₁ = -0,126ра²;     Х₂ = 0,343ра²;    Х₃ = 1,162ра;     Х₄ = -2,12ра.

Эпюры изгибающих моментов М_r и M_t для заданной системы приведены на рисунке б. Сравнение этих эпюр с эпюрами для аналогичной плоской пластины показывает, что благодаря наличию цилиндрического участка изгибающие моменты у заделки сильно снижаются. Так, например, у наружного края М_r = -0,138ра², тогда как в плоской пластине М_r = -0,5 ра².

В наиболее напряжённой точке, расположенной у нижнего края цилиндрического участка, изгибающий момент достигает величины М_r = 0,343 ра².

Исходные данные (задача 14б)