Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 4

Задача 7

Расчёт длинной цилиндрической оболочки, подкреплённой кольцами

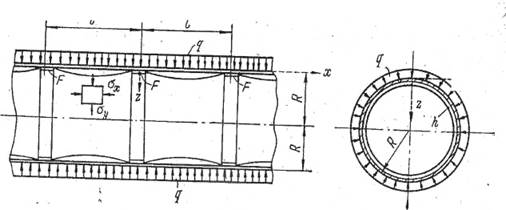
Цилиндрическая оболочка, подкрепленная равноотстоящими кольцами, площадь сечения которых F, подвергается внешнему равномерно распределенному радиальному давлению интенсивностью q (рис. 1). Для нахождения усилий и перемещений в любом сечении следует наложить решение для оболочки, загруженной равномерно распределённым радиальным давлением, на решение для оболочки, загруженной погонными моментами и поперечными силами по торцу.

Задача определения радиальных перемещений w для такой оболочки статически неопределима, и для её решения необходимо составить уравнение совместности деформаций. Рассмотрим отдельно два случая: кольцаабсолютно жёсткие и кольца могут деформироваться.   

Рис. 1. Схема оболочки, подкреплённой кольцами

1. Кольца абсолютно жёсткие. Силу взаимодействия, возникающую между кольцом и оболочкой, обозначим X: погонная поперечная сила Q₀ по схеме б равна половине силы взаимодействия Х: 

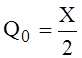                                                                                                                  (1)

Уравнение совместности деформаций имеет вид

                                                                               (2)

Оно представляет собой условие того, что радиальное перемещение оболочки в сечении х = 0, в котором расположено кольцо, произойти не может. Перемещение оболочки (w)^о_q от нагрузки q, которое было бы при отсутствии кольца, уничтожается перемещением оболочки , вызванным погонными усилиями Q₀ и М₀, возникающими в сечении х = 0 вследствие наличия в последнем подкрепляющего кольца.

Примечание. Верхние индексы «о» в формуле (2) показывают, что перемещения относятся к оболочке.

Радиальное перемещение оболочки от нагрузки q по безмоментной теории

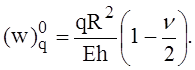
По ранее полученному решению радиальное перемещение оболочки от действия погонной поперечной силы Q₀ и погонного изгибающего момента М₀

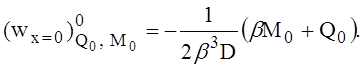
Подставив соответствующие выражения в уравнение (2), связывающее абсолютные значения перемещений, получим

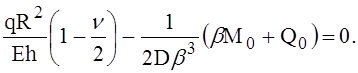                                                          (3)

Заменим Q₀ и М₀ в. этом уравнении на неизвестные силы взаимодействия X. Поперечная сила Q₀ связана с X зависимостью (1). Уравнение для замены М₀ на X найдём из условия, что в силу симметрии изгиба оболочки касательная к изогнутой срединной поверхности оболочки в сечении х = 0 должна быть горизонтальными (см. рис. 1):

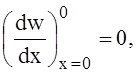
или на основании полученной ранее формулы

.

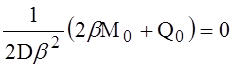С учётом формулы (1)

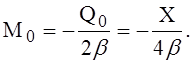                                                                                            (4)

Подставив в уравнение (2) выражения для Q₀ и М_о, получим

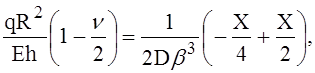
откуда

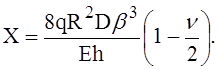
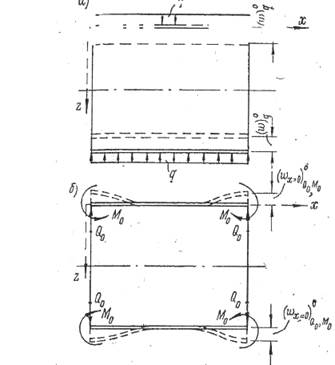
Рис. 2. К уравнениям совместности деформации для жёстких колец

Так как при помощи выражения для коэффициента затухания перемещений можно написать

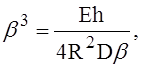                                                                                     (5)

то окончательное выражение для погонной силы взаимодействия

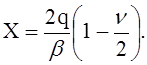                                                                                                     (6)

Тогда погонная поперечная сила Q₀ и изгибающий момент М₀ в сечении х = 0 по оси подкрепляющего кольца по формулам (1) и (4)

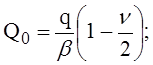                                                                                                   (7)

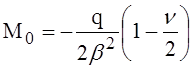                                                                                           (8)

Такие же выражения Q₀ и М₀получатся для цилиндрической оболочки, нагруженной радиальной сжимающей равномерно распределённой нагрузкой у защемленной кромки. Условия деформации у такой кромки те же, что и в случае абсолютно жёсткого подкрепляющего кольца.

2. Кольца могут деформироваться. В этом случае уравнение совместности деформаций следует записать так:

                                                                          (9)

Оно отличается от уравнения (2), так как радиальное перемещение оболочки, представленное левой частью уравнения (9), уже не равно нулю. Разность абсолютных величин перемещений оболочки, вызванных нагрузкой q и погонными усилиями Q₀ и М₀, должна быть равна обжатию кольца , вызванному погонной силой взаимодействия X (рис. 3).