Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 9

Задача 8

Сопряжение цилиндрической оболочки с полусферическим днищем

При действии на оболочку равномерно распределённого давления в местах нарушения непрерывности меридионального сечения возникают местные усилия — изгибающие моменты и поперечные силы. Например, оболочка, показанная на рис. 1, состоящая из цилиндрической части Ц и торцовой части Т в виде шарового сегмента, не имеет общей касательной в месте сопряжения этих частей. Поэтому по окружности CC их соприкосновения возникнут погонные усилия Q₀ и M₀. Объясняется это тем, что линейные перемещения wи углы поворота j касательных к изогнутой срединной поверхности, возникающие под действием равномерно распределённой нагрузки q, в общем случае различны для цилиндрической и торцовой частей оболочки. Для цилиндрической части радиальные перемещения обычно больше, чем для торцовой, а угловые равны нулю. У торцовой части могут возникнуть угловые перемещения по окружности СС. Поэтому, если мысленно отделить торцовую часть от цилиндрической по сечению С—С (рис. 2), в сечении возникнут линейный разрыв

                                                                                              (1)

и угловой разрыв

j = (j_т)_q                                                                                                                                                                                                 (2)

где       и  - радиальные перемещения цилиндрической и торцовой частей от нагрузки q;

(j_т)_q — угловое перемещение торцовой части от нагрузки q.

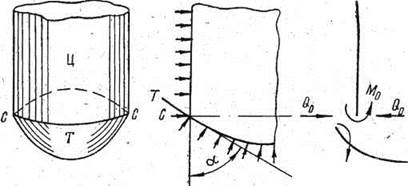
Рис. 1. Сопряжение цилиндрической оболочки с торцевой

Для уничтожения этих разрывов по сечению С-С необходимо приложить погонные поперечные силы Q₀ и изгибающие моменты М₀. Эти усилия вызовут в сечении следующие смещения: погонная поперечная сила Q₀ – линейные смещения  и  и угловые смещения (j_ц)_Q0 и (j_т)_Q0; погонный изгибающий момент М₀ — линейные смещения  и  и угловые смещения (j_ц)_M0 и (j_т) _M0. В общем случае эти смещения различны для торцовой и цилиндрической частей. Алгебраическая сумма линейных смещений должна равняться линейному разрыву D по формуле (1), а алгебраическая сумма угловых смещений — угловому разрыву из формулы (2).

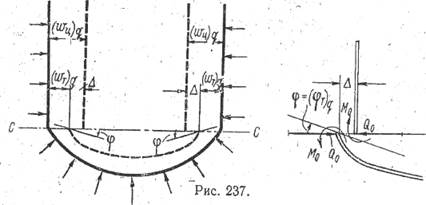
Рис. 2. Разность в радиальных смещениях

Таким образом, можно записать уравнения совместности деформации (рис. 3)

                                               (3)

                                                      (4)

Эти уравнения показывают, что возникающие в сечении С—С в непрерывной оболочке погонные усилия Q₀ и М₀ уничтожают линейный и угловой разрывы D и j и заставляют торцы цилиндрической и торцовой оболочек совпадать в переломе.

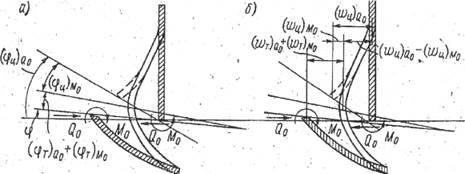
Рис. 3. Угловые (а) и линейные (б) перемещения

Приведённые рассуждения и уравнения (3) и (4) справедливы для сопряжения двух оболочек любого очертания и в частности для сопряжения цилиндрической оболочки с торцовой частью любого осесимметричного очертания — шарового, конического или плоского.

Рассмотрим случай наиболее простого сопряжения цилиндрической оболочки с полусферическим днищем и определим усилия Q₀ и М₀. В случае одинаковой толщины hцилиндрической и сферической частей можно считать, что по сечению С—С общая касательная для этих частей поворачивается в их сопряжении под действием усилий Q₀ на одинаковый угол и взаимный угол поворота отсутствует. Значит, в сечении С—С не возникает погонного изгибающего момента, т.е. М₀ = 0.

Остаётся только погонная поперечная сила Q₀, которую можно найти из решения геометрического уравнения (3), положив в нём члены, зависящие от М₀, равными нулю. Подставив в уравнение (1) абсолютные значения и  по ранее полученным формулам, найдём

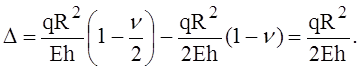                                                          (5)

Приняв во внимание, что изгиб около сечения С—С местный и достигает значительной величины как в цилиндрической, так и в сферической оболочке лишь вблизи от места сопряжения, условно заменим сферическую оболочку цилиндрической. В таком случае, подставив в уравнение (3) абсолютные значения =  по формуле (13) задачи 6 при М₀ = 0 иD по формуле (5), найдём