Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 18

Обозначив радиус сферы через а, будем иметь r₀ = asinj, при этом ширина элементарного кольца составит a·dj. Результирующая сил веса части купола, расположенной внутри угла j,

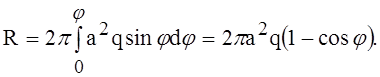
Тогда, согласно уравнениям равновесия, меридиональные N_j и тангенциальные (горизонтальные) N_q усилия определятся выражениями:

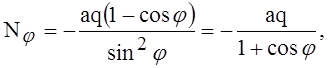                                                                (1)

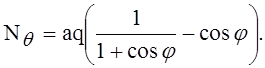
Здесь, как показано на рисунке, угол j отсчитывается от вертикали вниз.

Мы видим, что силы N_j получаются всегда отрицательными. Это значит, что по меридианам имеет место сжатие, которое возрастает по мере увеличения угла j. Для j = 0 имеем N_j = -aq/2, для j = p/2 сила возрастает вдвое: N_j = -aq. Силы N_q для малых углов j тоже отрицательны. Если 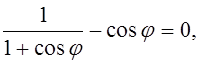 т.е. для j = 51⁰ 50’, N_q обращается в нуль и с последующим увеличением j становится положительной. Это указывает на то, что для j, превышающих 51° 50', в направлении, перпендикулярном к меридианам, имеются растягивающие напряжения.

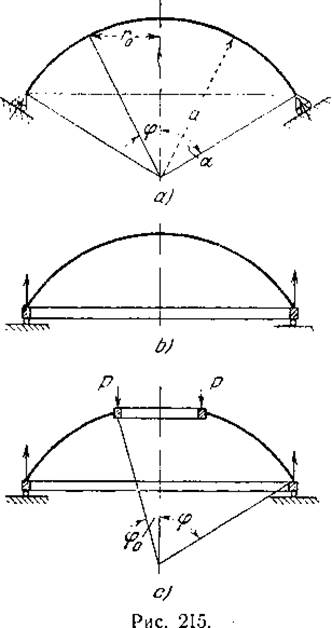
Вычисленные по уравнению (1) напряжения представляют собой весьма точные значения напряжений, фактически имеющих место в оболочке, если опоры её такого рода, что реакции направлены по касательным к меридианам (рис. 215, а). Обычно конструкция бывает такова, что на купол передаются лишь вертикальные реакции опор, горизонтальные же компоненты сил N_j  воспринимаются опорным кольцом (рис. 215, b), которое подвергается равномерному окружному (тангенциальному) растяжению. Так как деформация растяжения кольца обычно отличается от деформации, имеющей место в параллельном круге оболочки и определяемой выражениями (1), то около опорного кольца будет происходить некоторое изгибание оболочки. Исследование этого изгиба показывает, что в случае тонкой оболочки он имеет ясно выраженный местный характер и что на определённом расстоянии от опорного кольца уравнения (1) продолжают с удовлетворительной точностью представлять распределение напряжений в оболочке.

Зададим для определённости исходные данные: радиус купола а = 10 м; толщина h = 0,15 м; материал – железобетон; плотность r = 3,0 т/м³; угол a = 65⁰. Требуется рассчитать усилия в куполе и построить эпюры.

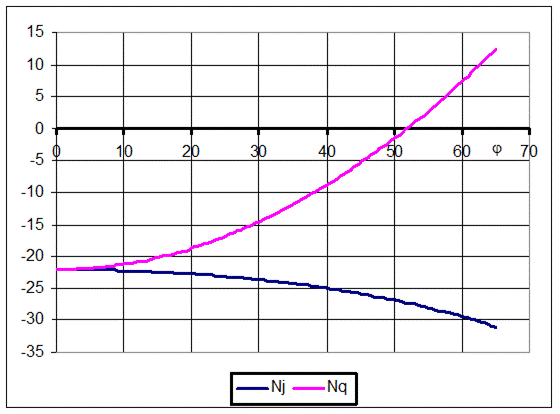
По результатам расчёта, масса купола составила 163 т, наибольшие напряжения (на нижней кромке купола) 207 кПа. Заметим, что прочность бетона на сжатие не меньше 25 МПа. Правда, здесь мы пренебрегаем изгибом оболочки.

Исходные данные (задача 12а)

Задача 12б

Сферический купол под действием ветровой нагрузки

Рассмотрим действие на оболочку давления ветра. Допустив, что направление ветра определяется меридианной плоскостью q = 0 и что давление его нормально к поверхности оболочки, мы будем иметь

                                                                             (1)

Уравнениями равновесия тогда будут

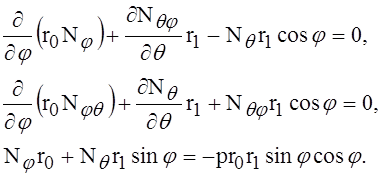                                                     (2)