Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 12

Таблица 2

a, град	Nm×103 MН/м	Sina - 0,707		NT×103 MН/м	формула
0	3,54	—	—	—3,54	(7) (5)
30	4,68	—	—	—4,68
45	7,20	0	0	—7,20
60	10,62	0,165	14,85	+4,23
90	13,50	0,295	26,55	+13,05

Погонное меридиональное усилие

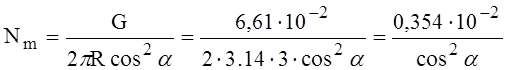                            (6)

Погонное окружное усилие из уравнения Лапласа

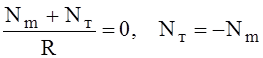                                                                             (7)

равно по величине и противоположно по знаку меридиональному.

Подсчёт значений погонных усилий N_m и N_тна участке СВ по формулам (6) и (7) выполнен в табл. 1 и 2. По данным этих таблиц построены эпюры усилий N_m и N_т (рис. 2).

            Рис. 2. Эпюры усилий в оболочке

Исходные данные (задача 10)

Фамилия	R, м	a0, град.	r, т/м3
Гунько	1,25	18	1,0
Дроздов	1,35	21	1,0
Дюба	1,5	24	1,0
Железнов	1,7	28	1,0
Кравченко	1,9	35	1,0
Купресов	2,1	42	1,0
Останин	2,4	48	1,0
Потенко	2,7	54	1,0
Царёв	3	58	1,0
Шкляр	3,5	64	1,0

Задача 11

а) Устойчивость круглого кольца постоянного поперечного сечения,

находящегося под действием равномерного давления

При достаточно малых давлениях кольцо в таких условиях испытывает равномерное сжатие. Сжимающая сила равна qr, где q - интенсивность внешнего давления, r – радиус кривизны кольца. Соответственно напряжения сжатия в нём равны

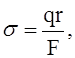
где F - площадь сечения кольца.

В любом сечении кольца изгибающие моменты и перерезывающие силы равны нулю. Если кольцо вывести из положения равновесия, заставив его немного изогнуться, то после снятия дополнительной нагрузки, вызвавшей этот изгиб, оно вернётся в положение равновесия. Но при увеличении давления наступает момент, когда круговая форма равновесия перестаёт быть устойчивой. Отклонения от круговой формы должны быть периодической функцией от угла , причём на длине окружности кольца должно укладываться целое число волн. Можно доказать, что величина давления, соответствующая искривлённой форме равновесия, определяется формулой

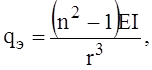где I – момент инерции сечения кольца, n – число волн, образующихся вдоль окружности кольца. Значение n = 1 соответствует перемещению кольца как твёрдого тела, так что минимальная эйлерова нагрузка будет при n = 2 (в этом случае один диаметр кольца уменьшается, а другой, перпендикулярный ему, увеличивается) и может быть рассчитана по формуле

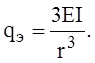
Для примера определим, на какой глубине произойдёт потеря устойчивости оболочки радиусом 2,5 м, толщиной 20 мм, подкреплённой кольцевыми шпангоутами в виде полособульба № 24б, расположенными на расстоянии 600 мм друг от друга.

Справочные данные:

высота профиля полособульба 240 мм, толщина стенки 14 мм, площадь сечения F = 43,55 см², отстояние центра тяжести от нижней кромки y₀ = 143,5 мм, собственный момент инерции i = 2542 см⁴.