Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 2

Две главные площадки оболочки вращения совпадают с экваториальным и меридиональным сечениями. Третья главная площадка нормальна к первым двум и параллельна срединной поверхности. При действии на оболочку внутреннего нормального давления элемент 1, выделенный у её наружной поверхности (рис. 3), находится в плоском напряжённом состоянии, а у внутренней поверхности (элемент 2) — в объёмном. Третья главная площадка испытывает главное напряжение -q, однако меридиональное и экваториальное напряжения, имеющие, как видно из уравнения Лапласа, порядок qR/h, значительно больше (в R/h раз), чем q. Поэтому обычно третьим главным напряжением q пренебрегают и считают, что материал оболочки по всей толщине стенки находится в плоском напряжённом состоянии.

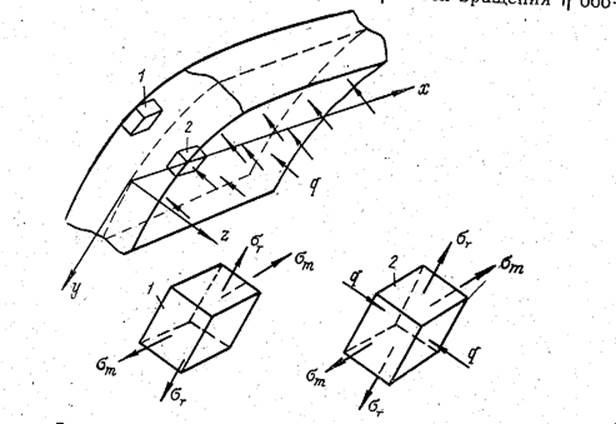
Рис. 3. Напряжённое состояние оболочки при внутреннем давлении

Исходные данные к задаче 5, а

Задача 6

Круговая цилиндрическая оболочка, загруженная

погонными моментами и поперечными силами по торцу

Рассмотрим оболочку настолько длинную, что усилия и перемещения на одном из концов не зависят от условий на другом конце. Будем называть ее длинной оболочкой.

Длинная оболочка с круглым поперечным сечением нагружена погонными изгибающими моментами М₀ и погонными поперечными силами Q₀ по торцу при х = 0 (рис. 1). Решение этой задачи служит основой для следующей задачи. Интенсивность радиальной нагрузки равна нулю; и поэтому дифференциальное уравнение, описывающее поведение оболочки, будет однородным:

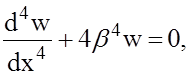                                                                                                   (1)

где 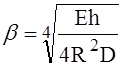 - коэффициент затухания перемещений; Е – модуль упругости материала оболочки; h - её толщина; 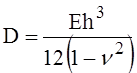 - цилиндрическая жёсткость; n - коэффициент Пуассона; R - радиус оболочки. Интеграл уравнения (1) не содержит частного решения и имеет вид

                   (2)

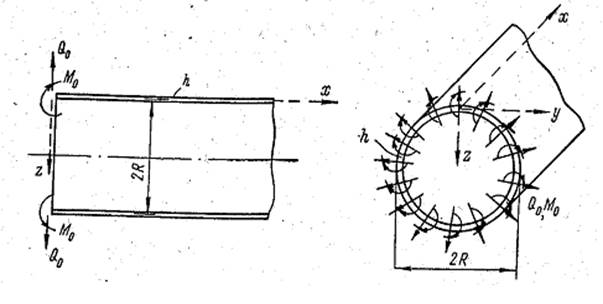
Рис. 1. Цилиндрическая оболочка, нагруженная погонными моментами и поперечными силами по торцу

Усилия М₀ и Q₀ вызывают местный изгиб, радиальные перемещения быстро затухают, и одно из условий для определения произвольных постоянных С₁,…,С₄ можно записать так: 1) при х → ∞ w→ 0. Ещё два условия можно записать для нагруженного торца; 2) при х = 0 М_х = М₀; 3) при х = 0 Q_x = Q₀. Четвёртого условия, как увидим, не понадобится. Действительно, при х → ∞

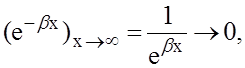
поэтому на основании первого условия получим

                                        (3)

Чтобы это условие соблюдалось, круглая скобка в выражении (3) должна быть равна нулю. Синус и косинус одновременно быть равными нулю не могут, следовательно, это условие возможно, только если С₁ = С₂ = 0. Тогда уравнение (2) принимает вид

                                                                     (4)

и для определения двух постоянных С₃ и С₄ достаточно двух условий: второго и третьего. Из второго условия найдём

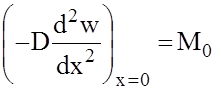                                                                                              (5)