Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 10

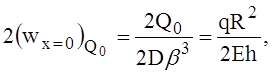
откуда

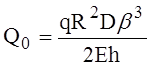                                                                                                    (6)

или, подставив в формулу (6) значение b³ по формуле (5) задачи 7,

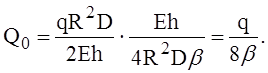
Таким образом, в случае сопряжения цилиндрической и полусферической оболочек одинаковой толщины, нагруженных радиальной сжимающей нагрузкой интенсивностью q, можно принять

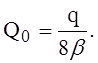                                                                                                              (7)

Выполним расчёт для оболочки со следующими характеристиками: диаметр D = 2440 мм (8 футов), толщина h = 12 мм, давление q = 500 кПа. Примем модуль упругости Е = 20000 МПа, коэффициент Пуассона n = 0,3.

Подставляя заданные величины в приведённые формулы, получаем: зазор, вызванный различной деформацией цилиндрической и сферической частей, D = 1,55 мм, цилиндрическая жёсткость D = 3,16 кН·м (не смешивать одинаковые обозначения диаметра и жёсткости!), параметр b = 10,6 м-1, погонная поперечная сила Q₀ = 5,88 кН/м. По этой силе легко рассчитать касательные напряжения, что здесь не сделано.

Исходные данные (задачи 8, 9)

Фамилия	D, мм	h, мм	q, кПа	h днища, мм
Гунько	2800	16	36	22
Дроздов	2600	16	34	20
Дюба	2400	14	32	20
Железнов	2200	14	30	18
Кравченко	2100	14	28	18
Купресов	1900	12	28	16
Останин	1800	12	26	16
Потенко	1600	10	25	14
Царёв	1400	10	24	14
Шкляр	1250	9	23	12

Задача 9

Сопряжение цилиндрической оболочки с плоским днищем

Оболочка нагружена внутренним радиальным давлением q. Плоское днище рассматривается как круглая пластина с радиусом R, нагруженная равномерным поперечным давлением q и погонным моментом М₀ по кромке. Ось направлена по радиусу пластины. Уравнение углов поворота пластины имеет вид

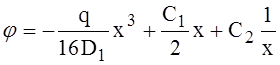                                                                          (1)

где D₁— цилиндрическая жёсткость пластины.

В центре пластины при х = 0 угол наклона касательной плоскости равен нулю, поэтому первое граничное условие j = 0 при х = 0, откуда С₂ = 0.

Выражение для радиального погонного изгибающего момента

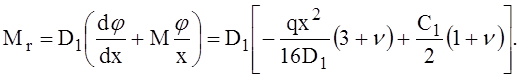
На контуре пластины, при х = R,

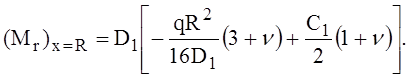
Этот погонный момент должен равняться и быть противоположным по знаку погонному моменту М₀, действующему по кромке оболочки, поэтому второе граничное условие (М_r)_x=R = М₀, откуда

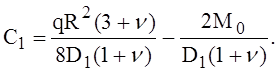                                                                          (2)

Подстановка значения С₂ = 0 и С₁ по формуле (2) в уравнение (1) даст следующее значение для угла поворота на контуре пластины:

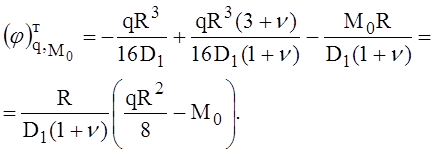                                           (3)

Радиальный изгибающий момент М_r в произвольном сечении пластины на расстоянии х от центра

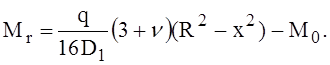                                                                (4)

Если считать радиальное перемещение пластины пренебрежимо малым в уравнении совместности (3), задача 8, можно принять  Тогда оно примет вид

                                                                                      (5)

Но 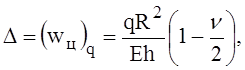 поэтому

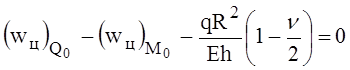
или, после подстановки значений радиальных перемещений w_ц цилиндра

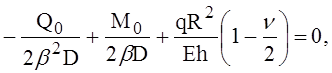                                                                (6)

где D— цилиндрическая жёсткость оболочки.

Уравнение (4) задачи 8 примет вид

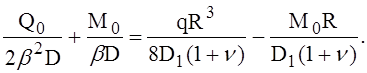                                                         (7)