Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 19

Пользуясь последним из этих уравнений, исключим силу N_q, в результате чего получим для определения N_q и N_qj = N_jq следующие два дифференциальных уравнения первого порядка:

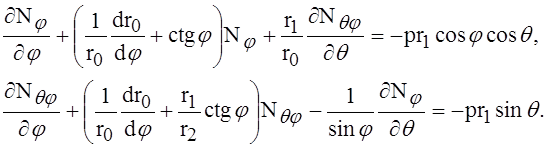                     (3)

Рассмотрим частную задачу в применении к сферической оболочке, для которой r₁ = r₂ = а. Возьмём решение уравнений (3) в виде

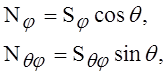                                                                                                 (4)

где S_j и S_qj суть функции одного лишь j. После подстановки в уравнения (3) получим для определения этих функций следующие обыкновенные дифференциальные уравнения:

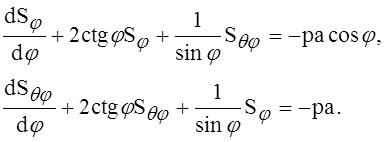                                                     (5)

Складывая и вычитая эти два уравнения и вводя обозначения

                                                                  (6)

получим два следующих обыкновенных дифференциальных уравнения, каждое из которых содержит лишь одно неизвестное:

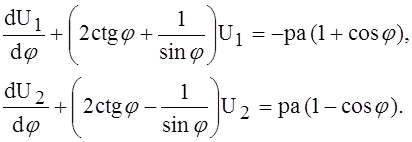                                                (7)

Применяя общее правило интегрирования дифференциальных уравнений первого порядка, получим

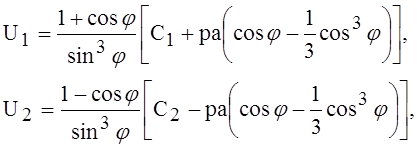                                               (8)

где С₁ и С₂ – постоянные интегрирования. Подстановка в уравнения (6) и применение уравнений (4) нам дадут в результате

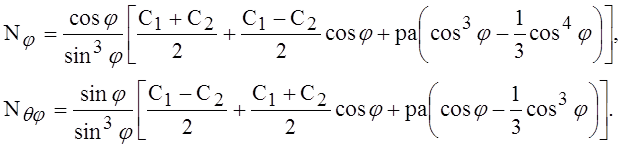            (9)

Чтобы определить постоянные интегрирования С₁ и С₂, рассмотрим оболочку, имеющую форму полусферы, и положим j = p/2 в выражениях (9). Тогда силы по экватору оболочки будут

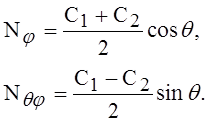                                                                                         (10)

Так как давление в каждой точке сферы имеет радиальное направление, то момент сил ветра относительно диаметра сферы, перпендикулярного к плоскости q = 0, равен нулю. Пользуясь этим обстоятельством и применяя первое из уравнений (10), получим

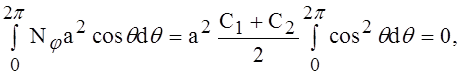
что даёт

С₁ = -С₂.                                                                                                                   (11)

Второе необходимое нам уравнение мы получим, взяв сумму компонентов всех сил, действующих на полусферу по направлению горизонтального диаметра в плоскости q = 0. Это даёт

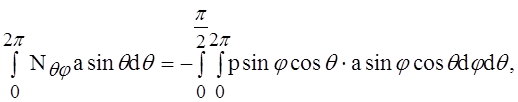
или

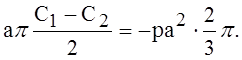                                                                                  (12)

Из (11) и (12) получим

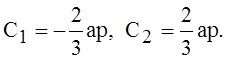
Подставив эти значения постоянных в выражения (9) и воспользовавшись третьим из уравнений (2), получим

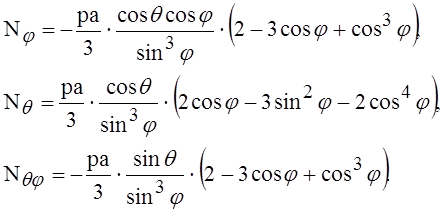                                         (13)

С помощью этих уравнений ветровые напряжения легко могут быть вычислены для любой точки оболочки. Если оболочка имеет форму полусферы, то нормальных сил по краю её не будет, поскольку . Силы сдвига N_qj по краю будут отличаться от нуля, по величине они будут равны, а по направлению противоположны равнодействующей давления ветра. Максимум абсолютных значений этих сил получится на концах диаметра, перпендикулярного к плоскости q = 0; в этой точке они равны ± 2ра/3.

Для примера рассчитаем усилия в оболочке, рассмотренной в предыдущей задаче. Примем скорость ветра равной 40 м/с, что соответствует скоростному напору

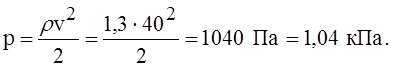
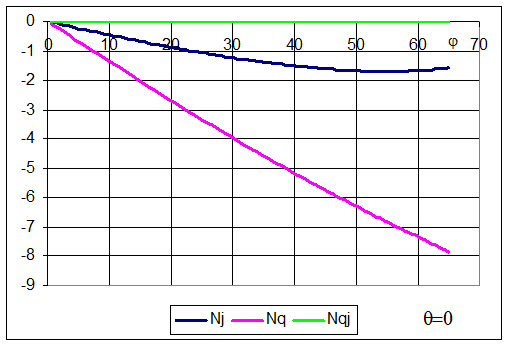
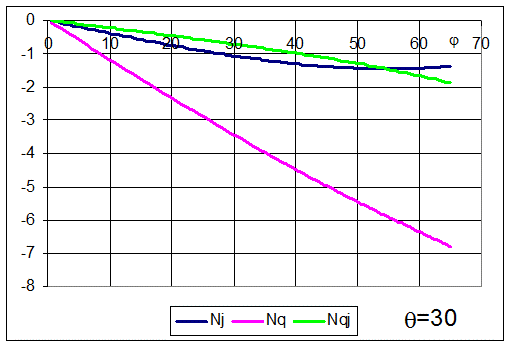
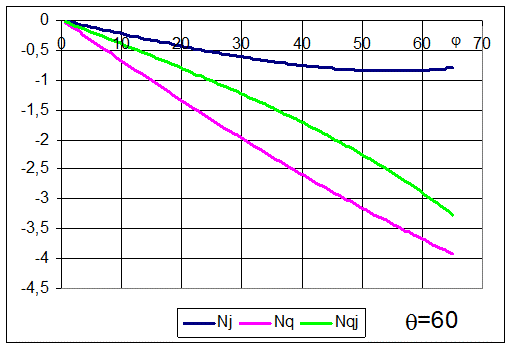
На следующих рисунках показаны зависимости N_j, N_q и N_qj от угла j (вдоль меридиана) для различных значений q (по окружности).

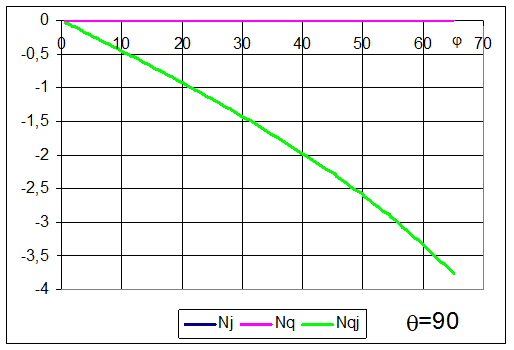
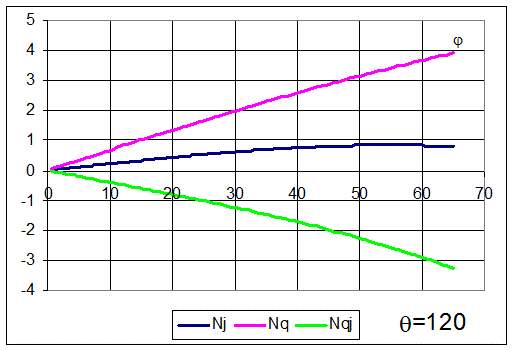
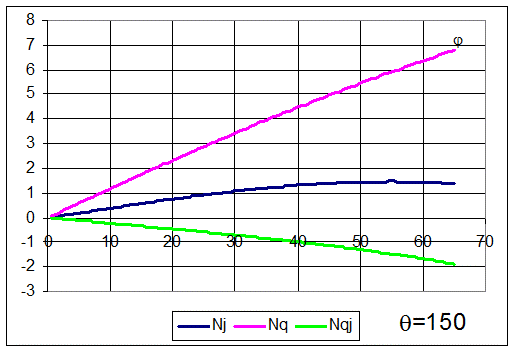
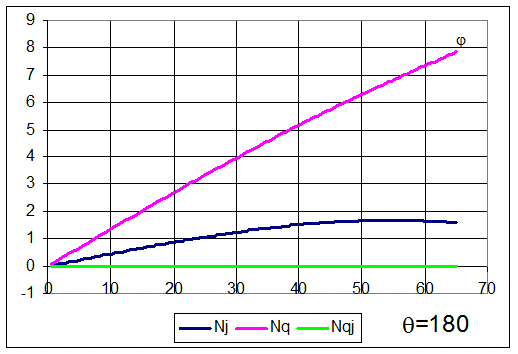
На последнем рисунке показаны зависимости N_j, N_q и N_qj при максимальных значениях j (по нижней кромке оболочки) от угла q (по окружности).

В заключение необходимо отметить, что задача решалась в предположении, что давление ветра является статическим, т.е. равномерно распределено по поверхности купола. В действительности это совсем не так. При обтекании купола потоком воздуха создаётся переменное поле скоростей и давлений, которое можно приближённо получить решением уравнений аэродинамики или экспериментальным путём. С наветренной стороны давление повышается по сравнению с атмосферным, с подветренной и сверху - понижается. Следовательно, реальная картина распределения усилий в куполе будет существенно отличаться от полученной приведённым расчётом.

Задача 12в

Оболочка вращения под ветровой нагрузкой