г) Устойчивость изогнутых по цилиндрической поверхности пластин,
сжатых вдоль образующей
Вопрос устойчивости изогнутых по цилиндрической поверхности пластин, сжатых вдоль образующей, представляет большой интерес для судостроения, поскольку при расчёте общей продольной прочности корпуса приходится проверять устойчивость скуловых листов его наружной обшивки, представляющих собой именно такие пластины.
В составе корпуса часто и кроме скуловых листов наружной обшивки можно встретить пластины, изогнутые по цилиндрической поверхности, которые приходится учитывать при проверке общей продольной прочности.
Решение задачи об устойчивости пластины, изогнутой по цилиндрической поверхности и сжатой вдоль образующей, можно получить, воспользовавшись уравнением устойчивости изотропной цилиндрической оболочки
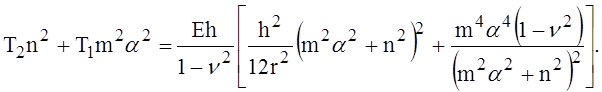
Будем рассматривать изогнутую по цилиндрической поверхности пластину, свободно опёртую на жёсткие продольные и поперечные рёбра, представляющие её опорный контур.
При этом продольные рёбра прямолинейны, а поперечные изогнуты по дуге окружности.
Будем считать, что пластина нагружена только сжимающими усилиями, действующими вдоль прямолинейных кромок, т. е.
T1 = ph и Т2 = 0.
![]() При потере устойчивости
такой пластины по её поверхности образуются выпучины и вмятины, в форме
волновой поверхности, причём вдоль прямолинейных кромок пластины образуется
целое число m полуволн, а вдоль изогнутых кромок также
целое число n1 полуволн.
При потере устойчивости
такой пластины по её поверхности образуются выпучины и вмятины, в форме
волновой поверхности, причём вдоль прямолинейных кромок пластины образуется
целое число m полуволн, а вдоль изогнутых кромок также
целое число n1 полуволн.
Примем следующие обозначения: а — длина прямолинейных кромок пластины; b — длина изогнутых кромок пластины.
Для того чтобы воспользоваться формулой для расчёта на устойчивость изогнутых цилиндрических пластин, свободно опёртых на продольные кромки, нужно положить
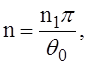
где q0 -центральный угол, соответствующий рассматриваемой пластине;
n1 — число полуволн. Так как q0r = b, то
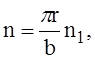 кроме
того, в принятых обозначениях
кроме
того, в принятых обозначениях
![]()
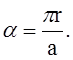
После преобразований получим
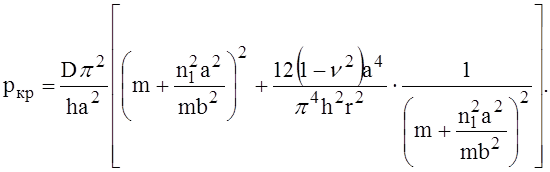
Полученное равенство представляет уравнение устойчивости изогнутой по цилиндрической поверхности пластины, сжатой вдоль образующей.
Нетрудно видеть, что в частном случае при r = ¥, когда рассматриваемая пластина становится плоской, второй член в квадратных скобках пропадает, и формула преобразуется в известную формулу устойчивости прямоугольных пластин
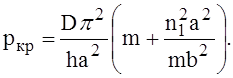
Присутствие второго слагаемого в квадратной скобке показывает благоприятное влияние кривизны пластины на её устойчивость, причём величина этого слагаемого, увеличивающего критическое напряжение пластины, растёт обратно пропорционально квадрату радиуса кривизны поверхности пластины.
Из общего уравнения устойчивости изотропной цилиндрической оболочки следует, что для изогнутой пластины, нагруженной поперечным давлением с выпуклой стороны и сжатой вдоль образующей, критическое сжимающее напряжение будет тем меньше, чем больше поперечная нагрузка.
Для определения критических напряжений изогнутой пластины необходимо определить числа полуволн m и n1, образующиеся при потере устойчивости пластины и соответствующие минимальному значению критических напряжений.
Перепишем уравнение в виде
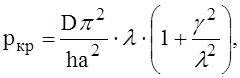 где
где
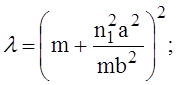
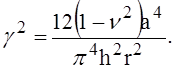
Очевидно, что при ![]() т.е. когда g меньше любого из возможных
значений l,
поскольку m и n целые числа,
критическое напряжение будет
т.е. когда g меньше любого из возможных
значений l,
поскольку m и n целые числа,
критическое напряжение будет
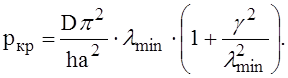
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.