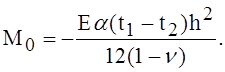Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 22

                                                                                     (2)

Реализация условий свободного торца требует здесь наложения моментов той же величины, но противоположного знака. Напряжения на свободном торце определятся поэтому путём наложения на напряжения (1) напряжений, вызванных моментами -М₀. Эти последние напряжения легко вычислить, пользуясь соответствующим решением, из которого следует, что

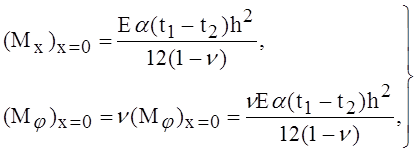                                               (3)

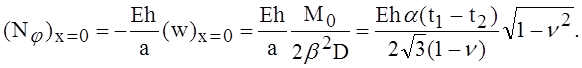              (4)

Здесь а – радиус оболочки.

Мы видим, что на свободном торце максимальное температурное напряжение действует в окружном направлении и получается путём сложения напряжений (1) с напряжениями, вызванными моментами М_j и силой N_j. Полагая, что t_l > t₂, получаем, таким образом,

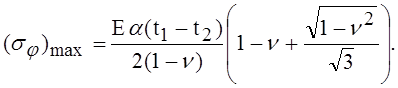                                                  (5)

При n = 0,3 это напряжение приблизительно на 25 % больше напряжения (1), вычисленного для точек, находящихся на большом расстоянии от торцов. Отсюда мы можем заключить, что если в каком-либо хрупком материале, например стекле, возникнет вследствие разности температур t₁ - t₂ трещина, то начнётся она с торца и будет следовать в осевом направлении. Подобным же образом можно вычислить напряжения также и для тех случаев, когда торцы защемлены или опёрты.

Градиент температуры в осевом направлении.

Если температура постоянна по толщине стенки, но изменяется по длине цилиндра, то задачу легко свести к решению уравнения

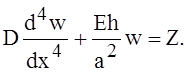
Пусть t = F(x) представляет собой повышение температуры оболочки, отсчитываемое от некоторой постоянной начальной температуры. Положим, что наша оболочка разбита плоскостями, перпендикулярными к оси х, на бесконечно тонкие кольца; тогда, обозначив радиус оболочки через а, мы сможем представить радиальное расширение колец вследствие изменения температуры в виде произведения 2aF(x). Это расширение можно уничтожить, вернув оболочку к её начальному диаметру путём наложения внешнего давления такой интенсивности Z, что

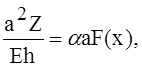
что даёт

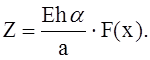                                                                                                    (6)

Нагрузка такой интенсивности полностью устраняет температурное расширение оболочки, вызывая в ней лишь окружные напряжения величиной

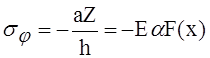                                                                                        (7)

Чтобы получить полные температурные напряжения, мы должны на напряжения (7) наложить напряжения, производимые в оболочке нагрузкой интенсивностью -Z. Эту последнюю нагрузку нужно приложить для того, чтобы освободить боковую поверхность оболочки от внешней нагрузки, данной уравнением (6). Напряжения, вызванные в оболочке нагрузкой -Z, получаются посредством интегрирования дифференциального уравнения

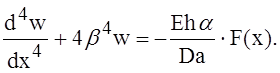                                                                          (8)

В качестве примера применения этого уравнения рассмотрим длинный цилиндр, подобный показанному на рисунке а, и положим, что часть цилиндра, лежащая вправо от поперечного сечения mn, имеет постоянную температуру t₀, между тем как температура левой части линейно падает до величины t_x на конце x = b согласно закону

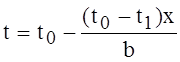
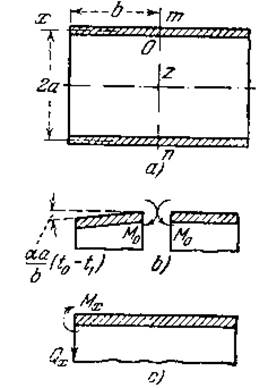
Изменение температуры в некоторой точке этой части цилиндра выражается, таким образом, формулой

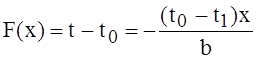                                                                               (9)

Подставив это выражение для изменения температуры в уравнение (8), находим, что частным решением этого уравнения будет

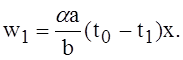                                                                                             (10)

Соответствующее этому частному решению смещение показано на рисунке b, из которого видно, что в сечении mn получается при этом угол разрыва, равный

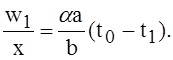                                                                                               (11)