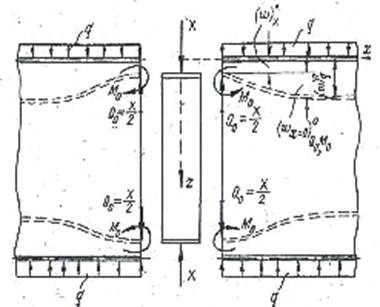
Рис. 3. К уравнениям совместности для упругих
колец
Радиальное перемещение точек кольца 
от погонной нагрузки X равно
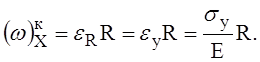
Сжимающее напряжение в кольце (рис. 4)
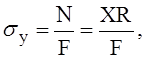
поэтому
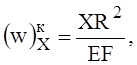
где F -— площадь поперечного сечения кольца.
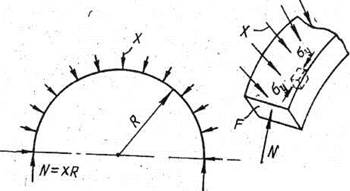
Рис. 4. К зависимости между радиальной нагрузкой и продольной силой в кольце
Выражения для Q0 и М0 через силу взаимодействия X остаются такими же [см. формулы (1) и (4)], так как условия симметрии сохраняются.
Если учесть значения всех величин, входящих в уравнение (9) совместности деформаций, получится выражение
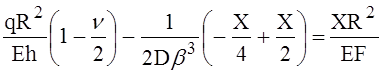(10)
Заменив b3 его выражением (5), произведя сокращение на R2/E и решив уравнение (10) относительно X, получим
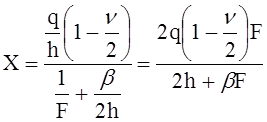. (11)
Представим решение (11) в виде произведения решения для абсолютно жёсткого кольца на коэффициент l, учитывающий податливость кольца:
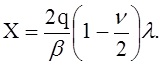(12)
Коэффициент
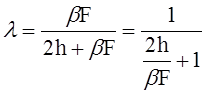(13)
учитывает уменьшение погонной силы X, получающееся при деформации подкрепляющего кольца. Оно тем ближе к единице, чем меньше толщина оболочки h и чем больше площадь сечения кольца F.
Зная X, по формулам (1) и (4) находим поперечную силу и изгибающий момент Q0 и М0 в сечении, в котором расположено кольцо. Зная величины Q0 и М0,можно найти возникающие от них радиальные перемещения и усилия Qx и Мх на любом расстоянии х от кольца, пользуясь формулами (10), (11) и (12) задачи 6.
Рассмотрим пример цилиндрической оболочки, подкреплённой кольцевыми рёбрами, при следующих исходных данных: радиус оболочки R = 5 м, её толщина h = 40 мм, рёбра выполнены в виде сварных тавров, размеры стенки 360×14 мм, полки 150×20 мм, расстояние между ними a = 700 мм. Давление на оболочку q = 4,0 МПа, что соответствует 400 м водяного столба. Задачу решить для случая абсолютно жёстких и реальных колец.
Вначале рассчитаем вспомогательные величины (вновь напомним о необходимости следить за размерностями подставляемых и получаемых величин).
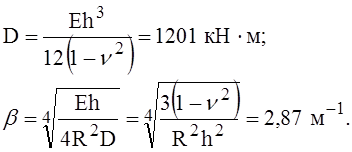
Выполним расчёты для случая жёстких колец.
Радиальное перемещение оболочки от нагрузки q
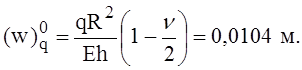
Погонная сила взаимодействия
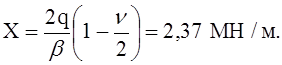
Погонная поперечная сила Q0 и изгибающий момент М0 в сечении по оси подкрепляющего кольца
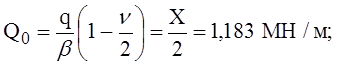
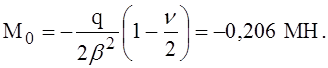
Наибольшие касательные напряжения в оболочке (на её срединной поверхности)
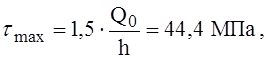
а наибольшие нормальные напряжения
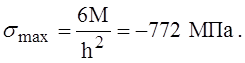
Обратим внимание на то, что касательные напряжения от сдвигающих усилий в оболочке невелики, что и следовало ожидать, учитывая её относительно небольшую толщину.
Задача для случая абсолютно жёстких колец решена. Теперь перейдём к случаю податливых колец.
Площадь сечения ребра складывается из площадей стенки и полки и составляет F = 80,4 см2.
Коэффициент, учитывающий уменьшение погонной силы X, получающееся при деформации подкрепляющего кольца
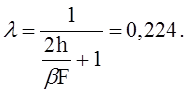
На этот коэффициент следует умножить все полученные результаты. Тогда имеем:
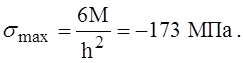
Как видим, в нашем случае подкрепляющие рёбра обладают значительной податливостью по сравнению с оболочкой и сильно уменьшают напряжения в ней по сравнению со случаем абсолютно жёстких рёбер. Но при этом в них самих также возникают сжимающие напряжения, которые рассчитаем по формуле
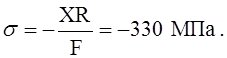
Задача решена. Но давайте вспомним, что в исходные данные входило расстояние между рёбрами, а в наших расчётных формулах оно никак не использовалось (если не считать того, что наличие одинаковых и равноотстоящих рёбер дало нам основание считать оболочку жёстко заделанной на них). Это ошибка или нет? Понятно, что расстояние (шпация) должно играть какую-то роль. Но какую?
Кроме предположения о жёсткой заделке, было сделано и другое предположение: о том, что на перемещения оболочки по линии присоединения ребра влияют только усилия взаимодействия с этим ребром. Это значит, что перемещения, вызванные соседними рёбрами, пренебрежимо малы по сравнению с перемещениями от этого ребра. Когда можно принять такое допущение? Из решения предыдущей задачи следует, что условием затухания перемещений будет неравенство
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.