Здесь дана, конечно, только схема потери устойчивости оболочки. Действительная же форма потери устойчивости оболочки будет зависеть от конструктивных размеров оболочки и размеров подкрепляющих её ребер и характеризоваться для различных оболочек различным числом волн, образующихся при потере устойчивости как по окружности оболочки, так и вдоль образующей.
Наибольший интерес для нас представляет вопрос установления величины внешнего давления для замкнутой цилиндрической оболочки, вызывающего потерю ею устойчивости.
Будем считать, что оболочка свободно опёрта по концам на две жёсткие поперечные стенки (переборки), так что перемещения v и w на них равны нулю.
Используя энергетический метод и принимая ряд допущений, получена формула для критического давления
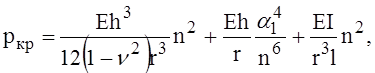
где n – число волн, образующихся при потере устойчивости оболочки, по её окружности;
m – число полуволн, образующихся по длине оболочки; оно чаще всего получается равным единице и в приведённой формуле отсутствует;
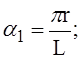
L – длина оболочки;
l - расстояние между подкрепляющими её рёбрами;
I – момент инерции ребра.
Число n должно быть таким, чтобы критическое давление получилось минимальным. Для этого получена формула
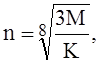
где 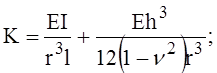
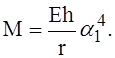
В выражении для К вторым слагаемым обычно можно пренебречь. Число волн, очевидно, должно быть целым.
Здесь предполагается, что при потере устойчивости рёбра деформируются вместе с оболочкой.
Для примера предлагается решить задачу при следующих исходных данных: L = 8 м; r = 2 м; l = 50 см; h = 12,5 мм; I = 1000 см4.
Вначале найдём число волн, образующихся при потере устойчивости по окружности оболочки, предварительно вычислив вспомогательные величины:
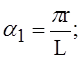
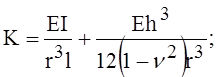
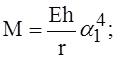
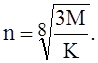
Число волн округляется до целого.
Теперь определим критическое давление оболочки
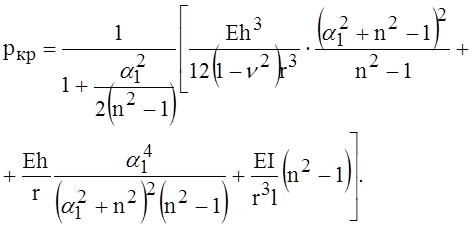
Выполним необходимые подстановки.
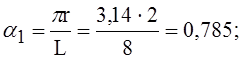
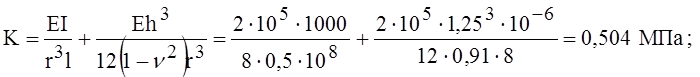
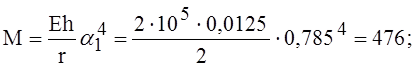
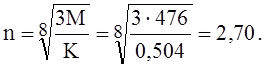
Так как число волн должно быть целым, примем n = 3.
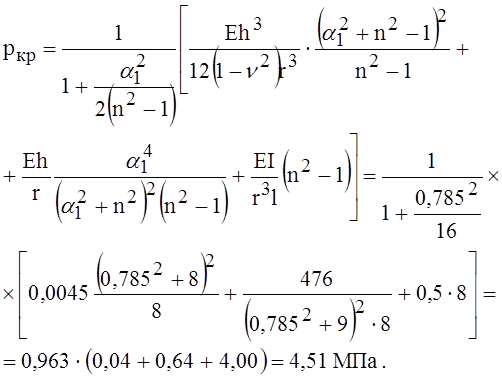
Чтобы убедиться в том, что потеря устойчивости оболочки происходит при трёх волнах, определим давление, соответствующее n = 2 и n = 4.
При n = 2 будем иметь ркр = 8,12 МПа, а при n = 4 ркр = 7,53 МПа.
Следовательно, критическое давление ркр = 4,51 МПа.
в) Устойчивость ортотропной цилиндрической оболочки
При исследовании устойчивости круговой цилиндрической оболочки, подкреплённой кольцевыми рёбрами жёсткости, мы предполагали, что форма потери устойчивости такой оболочки характеризуется одной полуволной по её длине и п волнами по окружности. Рёбра жёсткости при этом деформируются вместе с оболочкой.
В том случае, когда подкрепляющие оболочку рёбра обладают большой жёсткостью, возможна такая форма потери устойчивости, при которой рёбра сохраняют свою правильную круговую форму, а оболочка, теряя устойчивость, выпучивается между рёбрами.
Уравнение устойчивости оболочки в этом случае может быть получено из общего уравнения устойчивости, только при этом нужно полагать, что рёбра жёсткости играют роль концевых жёстких поперечных стенок, т. е. принимать L = l, где l — расстояние между рёбрами жёсткости,
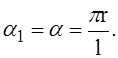
Кроме того, так как оболочка между рёбрами жёсткости не имеет никаких подкреплений, то в общем уравнении устойчивости нужно принять F = I = 0. Принимая во внимание также, что для оболочек, представляющих для нас наибольший практический интерес, число п достаточно велико (п > 10), в уравнении можно пренебречь единицей по сравнению с n2, после чего оно примет вид
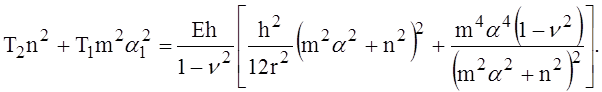
При действии всестороннего внешнего давления нужно принять T2 = pr, T1 = pr/2. Минимальное критическое давление получается при m = 1 и может быть определено по формуле
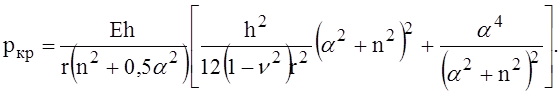
Отдельный вопрос – сколько волн n образуется по периметру оболочки при потере устойчивости. Его можно решать простым перебором значений, но число n может быть велико. Получена приближённая формула
![]()
где 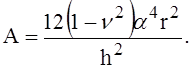
При некоторых допущениях для стальных оболочек критическое напряжение
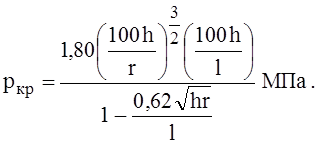
Знаменатель в этой формуле учитывает влияние продольной деформации.
Рассмотрим численный пример. Исходные данные примем по предыдущей задаче, исключив момент инерции ребра жёсткости (он в нашем случае не имеет значения), но радиус оболочки увеличим до 3 м.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.