Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 3

и после дифференцирования выражения (5)

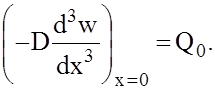                                                                                              (6)

Вычислим производные по x от выражения (4) для перемещения w:

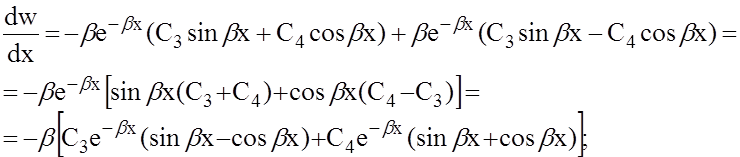
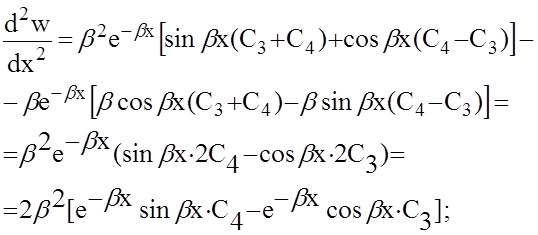
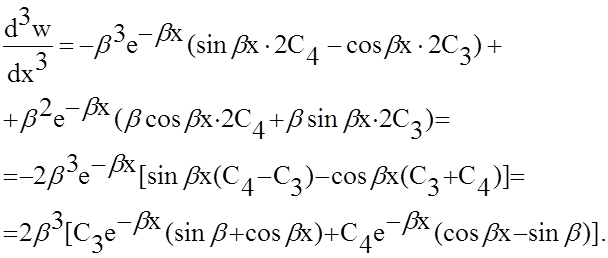
Произвольную постоянную С₃ найдем, подставив выражение для второй производной в условие (5). Учитывая, что синус нуля равен нулю, косинус — единице, а е⁰ = 1, получим

откуда

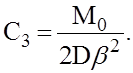                                                                                                              (7)

Подставив это выражение С₃ в выражение для третьей производной, найдем из условия (6) С₄,

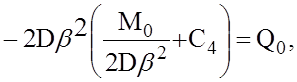
откуда

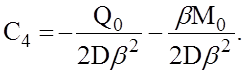                                                                                        (8)

Подстановка значений (7) и (8) в формулу (4) даёт уравнение изогнутой срединной поверхности оболочки

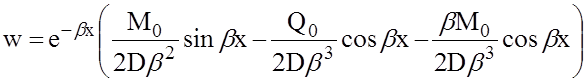
или

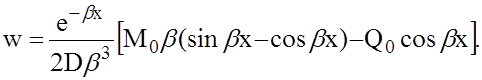                                         (9)

Выполнив соответствующие подстановки, получим для производных w

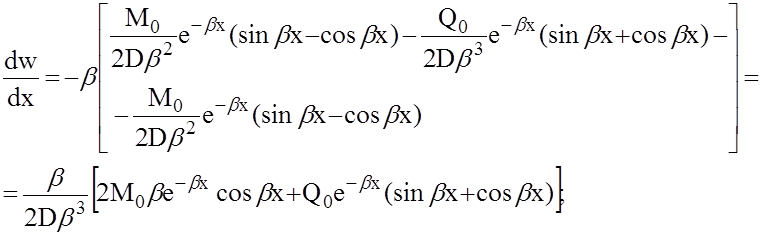аналогично

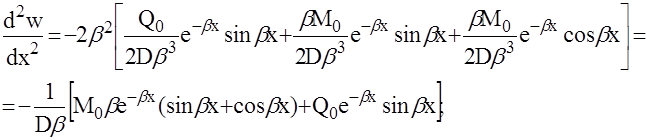
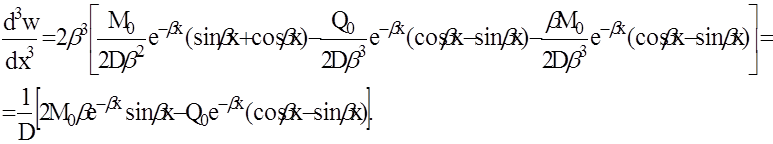
Введём для комбинаций показательной и тригонометрической функций bx, входящих в уравнения, следующие обозначения:

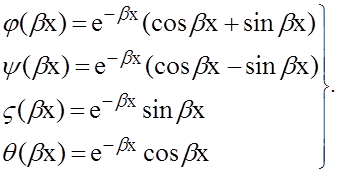
Тогда формула (9) для радиального перемещения напишется так:

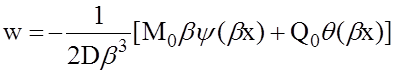                                                          (10)

и формулы для производных –

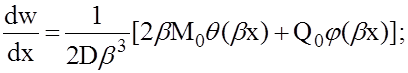
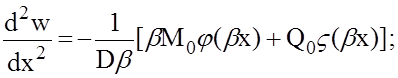
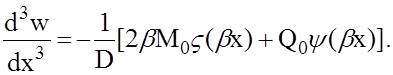
Имея выражения для перемещения w и его производных, можно, пользуясь соответствующими формулами, получить все усилия и перемещения в оболочке, в частности:

— угол наклона касательной к оси х

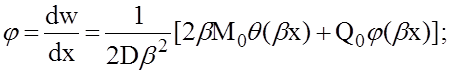
— изгибающий момент в меридиональном сечении

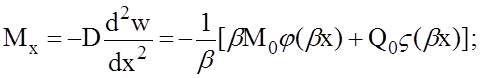                                         (11)

— поперечная сила в меридиональном сечении

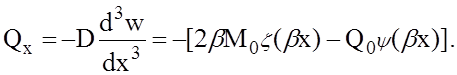                                              (12)

При βх > 0 все четыре функции по абсолютной величине меньше единицы. По мере возрастания х эти функции затухают, что подтверждает местный характер усилий и перемещений. При βх = 0 (а значит, и при х = 0), функции φ, ψ и θ равны единице, а функция z равна нулю. Поэтому на торце цилиндрической оболочки:

— радиальное перемещение

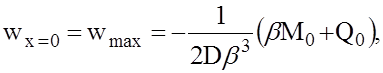                                                            (13)

где знак минус показывает, что при принятых за положительные усилия М₀ и Q₀ (см. рис. 1) и оси z, направленной по радиусу к центру кривизны, перемещение w происходит от центра (радиус R увеличивается);

— угол наклона касательной

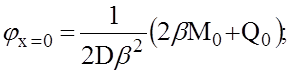                                                                               (14)

— изгибающий момент М_х и поперечная сила Q_x при х = 0 получаются равными заданным на кромке величинам М₀ и Q_0.

Обратим внимание на аналогию с решением для призматической балки, лежащей на упругом основании с коэффициентом жёсткости k.

Для полубесконечной балки, загруженной силой Р на конце, выражение для прогиба имеет вид:

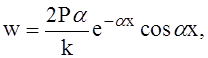
а для той же балки, загруженной концевым моментом М,

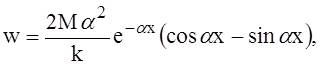
где 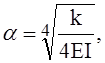 I – момент инерции поперечного сечения балки.

Для оболочки мы получили

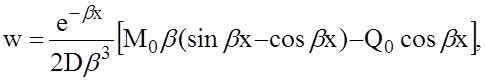
где .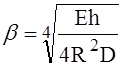

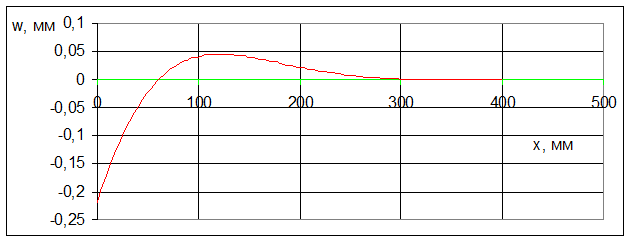
Рассмотрим пример оболочки при следующих исходных данных: радиус R = 0,8 м; толщина h = 12 мм; момент М₀ = 2,4 кН; сила Q₀ = 0,6 кН/м (напомним, что речь идёт о погонных нагрузках); модуль упругости Е = 205 000 МПа; коэффициент Пуассона n = 0,3.

Подсчитаем вспомогательные величины:

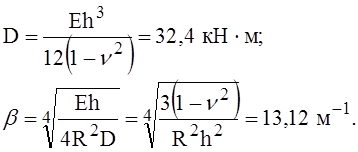
Вновь обратим внимание на необходимость строго следить за согласованием размерностей всех используемых и получаемых величин.

Теперь построим график перемещений, задав аргумент bx в пределах от 0 до 5:

Исходные данные (задача 6)

Фамилия	R, м	h, мм	M0, кН	Q0, кН/м
Гунько	0,55	4	0,3	0,2
Дроздов	0,75	5	0,5	0,3
Дюба	0,9	6	0,7	0,35
Железнов	1,1	6	0,7	0,35
Кравченко	1,35	7	0,9	0,4
Купресов	1,6	8	1,2	0,45
Останин	1,8	8	1,25	0,45
Потенко	2,1	9	1,5	0,5
Царёв	2,4	10	2	0,6
Шкляр	2,7	10	2	0,6