Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 21

Решение рассмотренной задачи о напряжениях в куполе под действием ветровой нагрузки можно получить также другим, более простым способом, а именно, рассматривая равновесие части купола, отсечённой по окружности текущего радиуса (рис. 2). Будем по-прежнему считать, что купол имеет сферическую форму и что р₂ = р₃ = 0 и

где

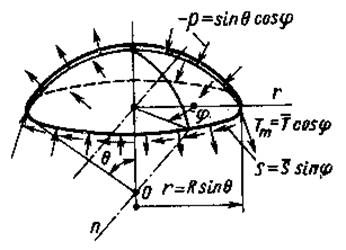
Рис. 2

Кроме давления р₁ на отсечённую часть действуют распределённые по краю силы Т_m и S.

Так как зависимость давления р₁ от угла j определяется законом косинуса, то очевидно, что меридиональное усилие Т_m (симметричный фактор) также изменяется по закону косинуса, а сдвигающее усилие S (обратно симметричный фактор) — по закону синуса, т. е.

Составим уравнения равновесия отсечённой части купола. Приравняв нулю сумму проекций сил на ось r, перпендикулярную оси оболочки, расположенную в плоскости j = 0, получим

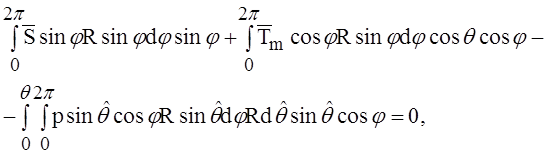
где

Выполнив интегрирование и произведя сокращения, найдём

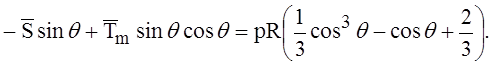
Второе уравнение получим, взяв сумму моментов сил относительно оси n, перпендикулярной плоскости j = 0 и проходящей через центр сферы:

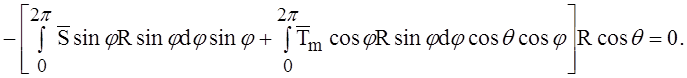
Момент сил давления относительно этой оси равен нулю, так как линия действия этих сил проходит через центр сферы. После интегрирования и сокращений найдём

Решение полученной системы двух уравнений даёт значения усилий

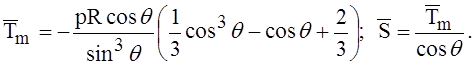
Окружное усилие T_t определяется по усилию Т_m на основании уравнения Лапласа:

Этот результат полностью совпадает с результатом, полученным методом интегрирования дифференциальных уравнений.

Исходные данные (задачи 12б, 12в)

Фамилия	Скорость ветра, м/с	Плотность воздуха, кг/м3
Гунько	15	1,3
Дроздов	16	1,3
Дюба	18	1,3
Железнов	20	1,3
Кравченко	22	1,3
Купресов	25	1,3
Останин	27	1,3
Потенко	29	1,3
Царёв	33	1,3
Шкляр	38	1,3

Задача 13

Температурные напряжения в цилиндрической оболочке

Равномерное распределение температуры.

Если цилиндрическая свободная по торцам оболочка подвергается воздействию равномерного изменения температуры, то никаких температурных напряжений в ней не возникает. Но если торцы её опёрты или защемлены, то свободное расширение оболочки станет невозможным и на торцах возникнут местные напряжения изгиба. Если температурное расширение оболочки со свободными торцами известно, то можно получить значения реактивных моментов и сил для любого способа симметричного опирания.

Градиент температуры в радиальном направлении.

Положим, что t₁ и t₂ - постоянные температуры стенки цилиндра соответственно на её внутренней и на наружной поверхностях и что по толщине стенки температура изменяется линейно; a - коэффициент температурного расширения. При этих условиях в точках, находящихся на значительном расстоянии от концов оболочки, изгиба не будет, и напряжения можно будет вычислить по формуле

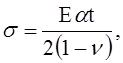
выведенной для защемлённой по краям пластинки. В таком случае напряжения на наружной и на внутренней поверхностях оболочки будут равны

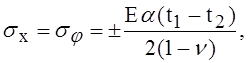                                                                                (1)

причём верхний знак относится к наружной поверхности, указывая на то, что при t₁ > t₂ на ней будут действовать растягивающие напряжения.

Вблизи торцов обычно имеет место некоторый изгиб оболочки, и потому полные значения температурных напряжений получатся в результате наложения на (1) напряжений, приводящих к выполнению заданных граничных условий. Рассмотрим для примера случай свободных торцов, у которых напряжения s_х должны отсутствовать. Приступая к анализу напряжённо-деформированного состояния, заметим, что напряжения (1) сопровождаются здесь появлением равномерно распределённых моментов М₀, величина которых равна