В нашей задаче 2p/b = 2,19 м, а расстояние между рёбрами = 0,70 м. Значит, соседние рёбра также вызовут деформацию оболочки на линии присоединения ребра, уменьшая обжатие оболочки и частично разгружая друг друга. Напряжения в оболочке также изменятся по сравнению с нашим расчётом, поскольку и изгибающие моменты от соседних рёбер не будут пренебрежимо малыми.
В этой задаче мы не будем рассчитывать напряжения, действующие вдоль оболочки, но заметим, что рёбра, подкрепляющие оболочку, частично уменьшают напряжения, действующие в кольцевых сечениях, но зато создают продольные напряжения. Правда, роль рёбер не ограничивается этим – они должны обеспечивать устойчивость оболочки, повышая её изгибную жёсткость.
Задача 7а
Цилиндрическая оболочка, подкреплённая шпангоутами
Замкнутая круговая цилиндрическая оболочка, ограниченная по концам поперечными переборками и не подкреплённая набором между переборками, при большом расстоянии между переборками неспособна воспринимать большое внешнее давление вследствие недостаточной устойчивости. Иными словами, состояние упругого равновесия такой оболочки возможно только при весьма незначительном наружном давлении. При повышении же этого давления сверх некоторого предельного значения состояние упругого равновесия такой оболочки будет нарушено и она, потеряв сначала свою правильную круговую форму, будет раздавлена.
Не останавливаясь пока на вопросе исследования устойчивости цилиндрической оболочки, отметим, что наиболее эффективным средством повышения устойчивости оболочки является подкрепление её кольцевыми поперечными рёбрами жёсткости, поставленными на равных расстояниях друг от друга в плоскостях поперечных сечений оболочки и имеющих, следовательно, круговую форму.
Следует отметить, что подкрепление оболочки круговыми рёбрами жёсткости, являясь необходимым средством обеспечения её устойчивости, нарушает нормальные условия работы оболочки, лишая её основных преимуществ по сравнению с пластиной, т.е. вызывает в ней явление изгиба.
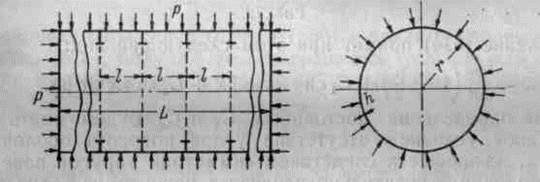
Рис. 1.
Рассмотрим задачу об определении усилий и деформаций в равномерно загруженной цилиндрической оболочке, подкреплённой равноудалёнными круговыми рёбрами одинаковой жёсткости (рис. 1).
Пусть расстояние между рёбрами жёсткости равно l, а площадь поперечного сечения каждого ребра жёсткости — F.
При действии на оболочку равномерного внешнего давления она будет сжиматься, так что диаметр её будет уменьшаться. В тех местах, где оболочка подкреплена рёбрами жёсткости, последние будут препятствовать её обжатию, нагружая оболочку усилиями обратного направления, распределёнными равномерно по всей окружности присоединения ребра жёсткости к оболочке.
Величина радиального перемещения оболочки будет наименьшей у рёбер жёсткости и наибольшей посередине промежутка между ними.
На некотором удалении от концевых переборок, ограничивающих рассматриваемую оболочку, радиальные перемещения оболочки будут симметричны относительно плоскости подкрепляющих её рёбер. Форма изогнутой оболочки будет иметь вид, показанный на рис. 2.
Поместив начало координат посередине расстояния между рёбрами жёсткости, мы, очевидно, должны в выражении для упругой поверхности оболочки коэффициенты С2 и С3 при нечётных функциях, нарушающих условие симметрии для перемещения w относительно начала координат, приравнять нулю. Выражение примет при этом следующий вид:
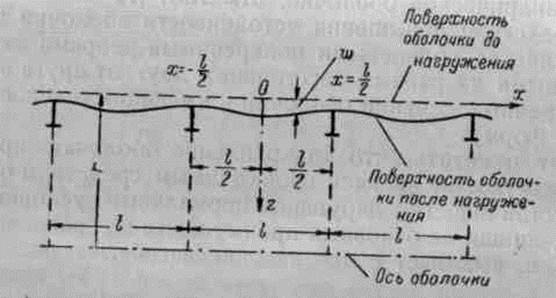
Рис. 2.
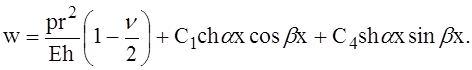 (1)
(1)
Здесь
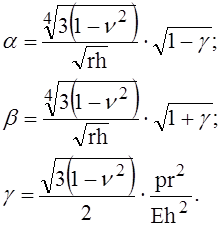 (2)
(2)
Для определения постоянных С1 и С4 будем иметь одно очевидное условие — отсутствие углов поворота оболочки на опорах, являющееся следствием симметрии упругой поверхности оболочки относительно плоскости каждого из подкрепляющих её рёбер, т.е.
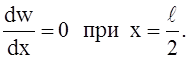 (3)
(3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.