Математика \ Прикладная математика и механика

Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 8

Для определения нормальных напряжений в меридиональных сечениях оболочки s2 рассмотрим относительную линейную деформацию по окружности сечения оболочки e2. Величина этой деформации связана с нормальными напряжениями в меридиональном сечении s2 и в поперечном сечении s1 законом Гука

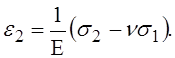                                                                                   (21)

Так как рассматриваемая деформация оболочки симметрична относительно оси и толщина оболочки мала по сравнению с радиусом, деформация e2 постоянна по толщине и равна соответствующей деформации срединной поверхности оболочки  

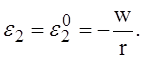                                                                                                      (22)

Из равенств (21) и (22) найдём

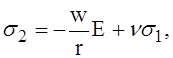                                                                                   (23)

следовательно, для определения напряжений s2 элемента оболочки необходимо предварительно определить радиальное его перемещение.

Величины интересующих нас перемещений определяются по выражению (1).

Для опорных сечений оболочки и сечений посередине пролёта нетрудно получить

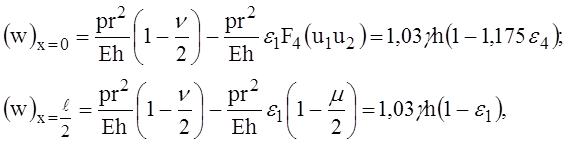                 (24)

где

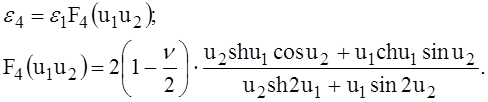                                (25)

На основании полученных выражений (24) для w можно определить нормальные напряжения в меридиональных сечениях оболочки по формуле (23).

Максимальные напряжения s2 будут, очевидно, на наружной и внутренней поверхностях оболочки.

Учитывая равенства (19), найдём

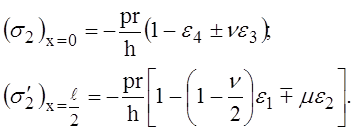                                                           (26)

Нормальные напряжения в поперечном сечении рёбер жёсткости, подкрепляющих обшивку, на основании выражений (6), (7) и (24) будут

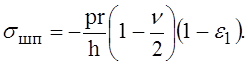                                                                              (27)

Зная нормальные напряжения в рёбрах жёсткости, можно на основании выражения (5) определить величину интенсивности давления оболочки на подкрепляющие её рёбра

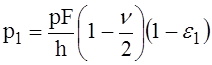                                                                         (28)

или, принимая во внимание выражение (10) и полагая n = 0,3, получить

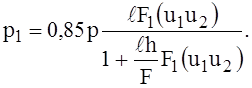                                                                             (29)

Пример. Определить расчётное напряжение в шпангоутах и обшивке цилиндрической оболочки при следующих исходных данных:

радиус оболочки                                   r = 175 см;

толщина оболочки                                h = 1,2 см;

расстояние между шпангоутами                l = 60 см;

площадь сечения шпангоута                      F=20 см2;

внешнее давление                                 p =1,25 МПа;

материал оболочки — сталь                   E = 2×105 МПа.

Определяем вспомогательные аргументы по соответствующим формулам.

g = 0,1098; a = 8,37; b = 9,34; u1 = 2,51; u2 = 2,80.

Вычисляем значения вспомогательных функций:

F1(u1u2) = 0,354; F2(u1u2) = 1,566; F3(u1u2) = 0,312; F4(u1u2) = -0.089.

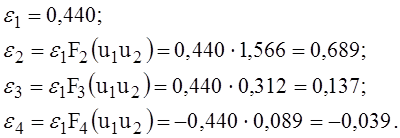
Определяем расчётные значения напряжений.

Напряжения в шпангоутах sшп = 86,8 МПа.

Напряжения в поперечных сечениях оболочки на шпангоутах = -216,8 / +34,5 МПа; в середине пролёта = -116,2 / -66,1 МПа.

Напряжения в меридиональных сечениях оболочки на шпангоутах = -76,4 / -151,8 МПа, в середине пролёта = -196,9 / -181,9 МПа.

Исходные данные (задачи 7, 7а)

Фамилия

R, м

h, мм

q, МПа

Стенка, мм

Полка, мм

а, мм

Гунько

3,2

16

1,25

250*12

120*16

600

Дроздов

3

14

1,3

240*10

120*14

600

Дюба

2,8

14

1,4

240*12

100*16

550

Железнов

2,6

12

1,8

220*9

100*14

550

Кравченко

2,4

14

2

240*10

110*12

550

Купресов

2,2

12

1,75

200*10

100*14

500

Останин

2

12

1,2

180*8

90*12

500

Потенко

1,8

10

1,4

180*9

90*12

450

Царёв

1,6

10

1,5

175*9

80*12

450

Шкляр

1,4

12

1,6

160*8

80*12

400
Скачать файл