Расчёт конической оболочки. Случай распределённой нагрузки. Расчет усилий в оболочке. Уравнение Лапласа, страница 11

Уравнения (6) и (7) содержат две неизвестные величины: М₀ и Q₀. Решая систему, находим погонную поперечную силу и изгибающий момент в сопряжении оболочки с плоским торцом (для случая D₁ = D):

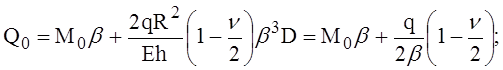                             (8)

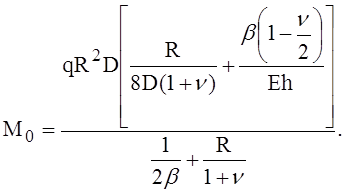                                                             (9)

В общем случае имеем:

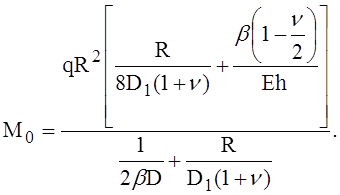                                                              (10)

Пользуясь выражениями радиальных смещений w и углов поворота j сечений оболочек и уравнениями (3) и (4) совместности деформаций из задачи 8, можно аналогичным путём вывести формулы для погонных поперечных сил Q₀и погонных изгибающих моментов М₀; возникающих в сопряжении цилиндрической оболочки с торцовой, имеющей форму полусферы, шарового сегмента, конуса или плоской пластины, при различных толщинах оболочки в цилиндрической и торцовой частях. Зная Q₀ и М₀, можно вычислить w_x, Q_x и М_х в любой точке цилиндрической части, пользуясь соответствующими формулами.

Для примера выполним расчёт оболочки, характеристики которой приведены в предыдущей задаче, но при толщине плоского днища 14 мм. Давление примем равным q = 50 кПа.

Вначале рассчитаем вспомогательные величины:

D = 31,6 кН·м;

b = 10,62 1/м;

D₁ = 50,3 кН·м.

Теперь выполним подстановки и найдём усилия, действующие по линии сопряжения оболочки с днищем:

Погонный изгибающий момент М₀ = 8,63 кН;

Погонная поперечная сила Q₀ = 94,9 кН/м.

Тогда напряжения в оболочке составят: нормальные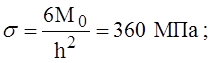   

касательные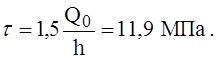

Задача 10

Полусферический сосуд под гидростатической нагрузкой

Тонкостенный сосуд, выполненный в виде полусферы, свободно закреплён по диаметральной окружности и частично нагружен, как показано на рис. 1, а, водой плотностью r = 1,00 т/м³. Пренебрегая собственным весом сосуда, построить эпюры изменения главных напряжений.

Для получения решения рассмотрим отдельно участок сосуда, испытывающий давление жидкости, и участок, не испытывающий этого давления (рис. 1).

1. 45 <a< 90° (участок ВА).

Из условия равновесия отсеченного от сосуда сегмента, показанного на рис. 1, б, меридиональное погонное усилие

.

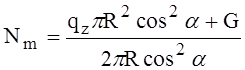Рис. 1. Схема сосуда с жидкостью

Вес G равен объёму шарового сегмента высотой y, умноженному на объёмный вес:

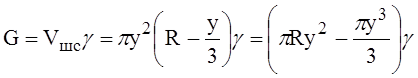                                              (1)

Выразим радиус R через размеры у и a. Из прямоугольного треугольника

откуда 

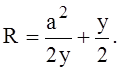
Подставим это выражение в формулу (1):

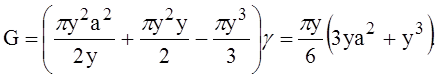
Учитывая, что у = R(1 - cos j) и a = R sin j , получим

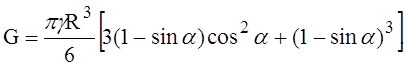                                                 (2)

Выразим через R и a интенсивность нагрузки q:

 (3)

Подстановка найденных выражений (2) и (3) для G и q в соответствующую формулу даст погонное меридиональное усилие

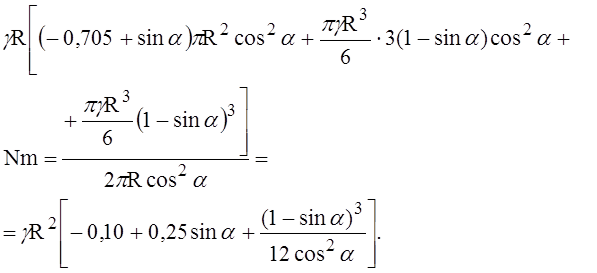            (4)

Общий, множитель

Окружные погонные усилия N_т находим из уравнения Лапласа, полагая в нём R₁ = R₂ = R = 3 м и подставляя найденное значение (4) меридиональных усилий N_m:

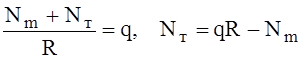, или, подставляя вместо q его выражение (3),

                                                                      (5)

Подсчёт значений погонных усилий N_m и N_т на участке ВА по формулам (4) и (5) выполнен в табл. 1 и 2.

2. 0<a<45° (участок СВ).

Высота жидкости в сосуде

H=R(1 —sin 45°) = 3 (1 —0,707) =0,879м;

Вес G жидкости, находящейся в сосуде,

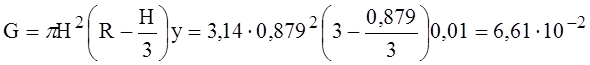МН.

Таблица 1

	sin a	cos a	(1-sina)	cos a	0,25sima			Nm×103 МН/м	Формула
0	—	1,000	—	1,000	—	—	—	3,54	(6) (4)
30	—	0,870	—	0,755	—	—	—	4,68
45	0,705	0,705	0,256	0,496	0,176	0,0040	0,080	7,20
60	0,870	0,500	0,0022	0,250	0,217	0,0007	0,118	10,62
90	1,000	0	0	0	0,250	0	0,150	13,50