Конспект лекций по теории электрической связи, вторая часть, страница 6

6.  Для большинства случайных процессов, стационарных и эргодических, выполняется свойство . Т.е. ФАК – убывающая, стремится к нулю. Однако убывание не обязательно монотонно.

Пример:

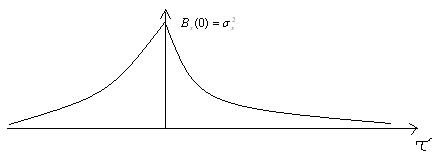
1. , , - интервал корреляции случайной величины.

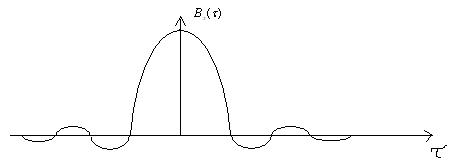
2. Может быть и отрицательной, в пределах убывает не монотонно, но стремится к нулю.

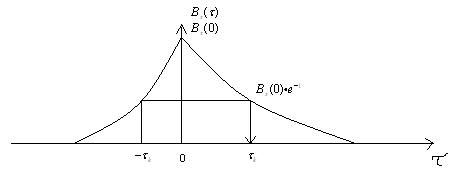
Интервал корреляции

Есть несколько определений понятия интервал корреляции, так же как и несколько определений для полосы пропуская фильтра.

Определение 1. Интервал корреляции определяется как такое значение временного сдвига , при котором значение коэффициента корреляции равно:

,

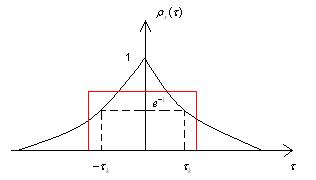
Определение 2 (наиболее универсальное определение).

Упражнения

Законы распределения вероятности и числовые характеристики случайных процессов

Виды случайных процессов:

1.  Случайный процесс с равномерной плотностью вероятности в замкнутом интервале значений (равновероятный случайный процесс)

2.  Нормальный случайный процесс (Гауссовский случайный процесс)

3.  Гармонические колебания с равновероятной случайной фазой (закон арксинуса)

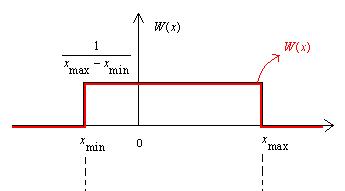
Случайный процесс с равновероятным распределением.

, процесс стационарный следовательно