Конспект лекций по теории электрической связи, вторая часть, страница 25

  Если происходят 2 независимых события, то количество информации равно сумме информаций, которое несет каждое из этих событий.

Доказано, что количество информации будет некоторой функцией

X      p_x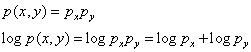                                        

Y      p_y

                                           Частные количества информации

Х – некоторое событие, которое может иметь L исходов. Вероятность каждого исхода: p_i; (i – номер исхода)

Тогда количество информации, которое содержится в этом исходе:

L-значений частного количества информации. Так как процессы случайные, будем рассматривать среднее статическое количество информации.

                 Среднее количество информации (энтропия)

Энтропия есть математическое ожидание от всех частных количественных информаций.

Таким образом, энтропия

(среднее количество информации, которое несет в себе событие, имеющее L исходов).

                          Единицы количества информации

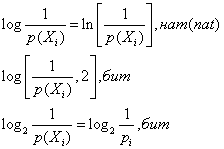
Пример:

Тогда

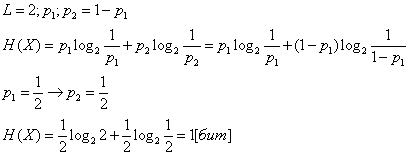
Пусть теперь L возможных исходов, вероятность исхода

                          Энтропия источника сообщения.

Пусть ИС имеет объем алфавита L=32=2⁵ (без пробела и без буквы «ё»), n - длина сообщения (число буквенных символов), число букв может быть произвольным. Поэтому в определении энтропии от n надо избавиться. В дальнейшем не будем применять значение «буква» (будем говорить «символ»).