Конспект лекций по теории электрической связи, вторая часть, страница 3

1)

2) неубывающая функция своего аргумента

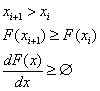
3)  F(x)=0  X<x

4)  F(x=1)  X<x

Свойства плотности вероятности.

                                                                    

1)

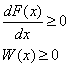
2) W(x);    

Площадь под графиком, плотность вероятности всегда единица.

(рисунок)

Двумерные и многомерные.

Для описания динамики поведения случайных процессов нужно рассматривать двумерные функции распределения вероятностей или многомерные.

                                                                   

Аналогично многомерные:

Самым общим описание случайного процесса является n-мерная функция распределения вероятности при .

Числовые характеристики случайных числовых процессов.

n=4           X(t) и Y(t)

1)Математическое ожидание случайных процессов – это усредненное по всему множеству реализаций поведений случайного процесса.

Дисперсия и среднеквадратичное значение случайного процесса.

Дисперсия случайного процесса X(t) обозначается

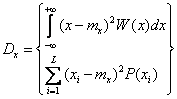непрерывный случайный процесс [B*B=Bт/Ом]

Физический смысл дисперсии – это математическое ожидание квадрата отклонений мгновенного значения случайной величины относительно ее математического ожидания.