Самое большее, что можно в условии
случайного процесса определить (принять решение, зная 
-
априорную и 
- апостериорную вероятности).
Допустим: 
1 и 0 передаются
равномерно, а шум
мал.
при 
.
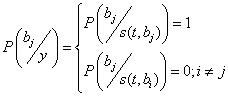
Условия для априорных и апостериорных вероятностей.
(y-одно и тоже для всех j).
В основе всех Байесовских алгоритмов лежит задача определение апостериорных вероятностей.
Как учесть, что цена ошибочного принятия решения в различных условиях может быть различна.
Цена ошибок задается матрицей:
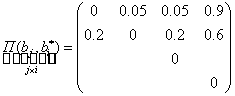
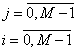
М=4
Нули в матрице говорят, что правильные решения не несут потери.
0,9- все потери из-за принятия этого решения.
На оставшиеся в строке по 0.05 ( 5%). В строке сумма элементов должна быть равна 1.
Матрица потерь, матрица штрафов, матрица рисков – названия одной матрицы П.
-
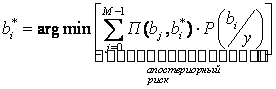
что на самом деле передавалось, надо найти;
-
что конкретно передавалось.
Чтобы построить реальный алгоритм, нужно знать апостериорную вероятность.
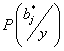
На практике применяют 2 варианта матрицы штрафов (рисков). В соответствии с этим, 2 частных критерия, следовательно, из критерия минимального риска:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.