Конспект лекций по теории электрической связи, вторая часть, страница 39

Далее можно привести как минимум 4 частных формулировки этой теоремы.

1-ая формулировка. Дискретный источник сообщений  и дискретный канал. Если производить источник дискретных сообщений меньший  пропускной способности дискретного канала  ()  то существуют такие методы создания  кодеров источника  и как кодеров при передаче и соответственно  такие ДКК и ДКИ , при которых возможна передача дискретных сообщений со сколь угодно малой вероятности ошибки , при скорости передачи сколь угодно близкой к  пропускной способности канала. R- скорость передачи(бит/c )

Существуют такие КИ И КК – методы помехоустойчивого кодирования.

Модулятор и демодулятор в обсуждении не участвуют, так как они вложены в правую часть неравенства , т.е. в пропускную способность дискретного канала.

2)Дискретный источник и дискретный непрерывный канал.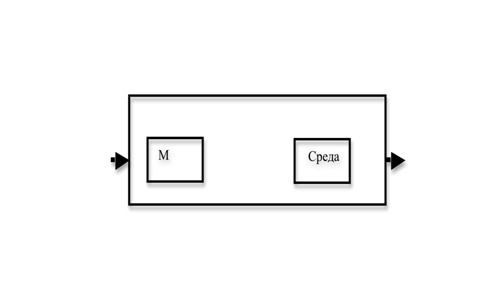

3)Дискретный источник и непрерывный канал.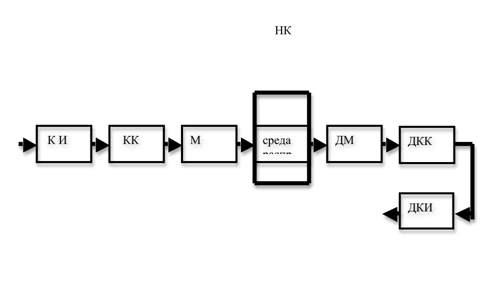

4)Непрерывный источник и непрерывный канал.

1.  Определения понятия энтропии источника непрерывных сообщений.

2.  Основные примеры энтропии для различных источников непрерывных сообщений.

3.  Формулировка второй основной теоремы Шеннона применимой к непрерывным источникам непрерывного канала.

4.  Пример применения этой теоремы .

1.Определения и понятия энтропии источника непрерывных сообщений.

Пусть  и  - 2 непрерывных случайных процесса. Если эти 2 случайных процесса так похожи друг на друга , что различия между ними несущественно , то такие 2 реализации эквивалентны. . Здесь важен критерий эквивалентности.

Е-энтропией источника непрерывных сообщений называется энтропия этого источника при заданном критерии эквивалентности. Тогда Е-энтропия определяется как  то минимальное необходимое количество информации.