Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 9

Теорема 2. Множество точек, координаты которых удовлетворяют линейному неравенству  есть полуплоскость с границей  (знак неравенства может быть и противоположным).

Доказательство. Положим для определенности  и обе части неравенства разделим на b. В зависимости от знака b получим

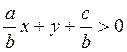 или 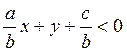. Обозначив 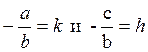, последнее неравенство записать так: > или

__________________________________

^х § 1.3. мы использовали  термин «линия» (или «кривая»), а здесь встретилось понятие «непрерывная линия». Строгое определение этих понятий сложно и потому в начале курса мы ограничимся имеющимися у каждого человека интуитивными представлениями.

^хх Понятие непрерывной функции двух переменных рассматривается в курсе математического анализа. Непрерывность означает, что малые изменения аргументов вызывают малое изменение функции.

Легко видеть, что этому неравенству удовлетворяют координаты точек, лежащих выше (или ниже) прямой . А множество так х точек представляет собой полуплоскость с границей .

Теорема доказана. В ходе доказательства мы воспользовались известным из школьного курса уравнением прямой . В главе 3 уравнение прямой будет изучено подробно.

Пример 3. Изобразить на чертеже множество точек, координаты которых удовлетворяют неравенству 2х + у – 4 > 0.

Решение. По теореме 2 искомым множеством будет одна из полуплоскостей, ограниченных прямой  : 2х + у – 4 = 0. Прямую построим по двум точкам, например, (0, 4) и (2, 0). Остается определить, какую из двух полуплоскостей  определяет данное неравенство. Координаты точки 0(0,0) неравенству не удовлетворяют. Поэтому искомой полуплоскостью является не та, в которой лежит начало координат, а другая (рис. 1.20).

Пример 4. Изобразить на чертеже множество точек, координаты которых удовлетворяют неравенству х² – у² < 0.

Решение. Линия : х² – у² = 0 или (х – у)(х + у) = 0 распадается в пару прямых х –у = 0 и х + у = 0, биссектрис координатных углов. В данном случае плоскость разбивается на 4 области (рис. 1.21). Проверяя по одной точке из каждой области (можно взять, например, точки А₁(1, 0), А₂(0, 1), А₃(-1, 0), А₄(0, -1)), видим на основании теоремы 1, что неравенству удовлетворяют координаты точек лишь тех областей, которые содержат А₂ и А₄.

                                                   у                                                          у

                                                                                                               А₂

                          А                   4 ·                                                           А₃                А₁

                          М                                                                                               х

                                                                                                               А₄

                       В     α                       2 ·                       х

                                                о

Рис. 1.19                                  Рис. 1.20                                  Рис. 1.21

§ 1.7. Аффинные координаты

Прямоугольные декартовы координаты дают пример важнейшей, но не единственной системы координат, которая употребляется в математике и в практической деятельности. В этом и следующем параграфах мы рассмотрим другие системы координат на плоскости.

Аффинная система координат получается путем естественного обобщения прямоугольной декартовой. Она тоже задается осями координат и единичными отрезками на них, но здесь оси пересекаются под произвольным углом и не требуется равенство единичных отрезков ОЕ₁ и ОЕ₂ (рис. 1.22). Координаты произвольной точки М определяются также, как и прямоугольные декартовы координаты: через точку М проводятся прямые параллельно осям; эти прямые пересекают оси и ординат в точках М₁ и М₂ соответственно: координаты точек М₁ и М₂ на осях принимаются за аффинные координаты точки М на плоскости.