Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 4

Задача 2. Найти координаты точки М, делящей отрезок АВ в отношении λ, если А(х₁, у₁), В(х₂, у₂).

Решение. По определению (§ 1.1.) точка М лежит на отрезке АВ и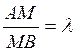

Если АВ || ОУ, то обозначим проекции точек А, В и М(х, у) на ось ОХ через А₁, В₁ и М₁ соответственно (рис. 1.8) Согласно определению координат точки на плоскости эти проекции, будучи точками оси ОХ, имеют следующие координаты: А₁(х₁), В₁(х₂), М₁(х).

Так как 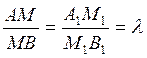 (теорема о пропорциональных отрезках), то точка М₁ делит отрезок А₁В₁ в том же отношении λ. Поэтому координата х определяется формулой (1.1.2). Если кроме того АВ ||ОХ, то верна аналогичная формула для у. Итак,

                    (1.2.3)

Мы получили формулы деления отрезка в данном отношении. Они остаются в силе и тогда, когда отрезок АВ параллелен какой-либо оси. Например, если АВ || ОХ, то у=у₁=у₂. Вторая формула (1.2.3.) при у₁=у₂ дает тот же результат.

Частный случай последних формул – формулы деления отрезка пополам,  получившиеся при λ=1:

                      (1.2.4)

Их словесная формулировка: координаты середины отрезка равны полусуммам соответствующих координат его концов.

Впоследствии (§ 2.6.) понятие деления отрезка в данном отношении будет обобщено и будет дан другой вывод формул (1.2.3)

Задача 3. Найти площадь треугольника с вершинами А(х₁, у₁), В(х₂, у₂), С(х₃, у₃).

Решение, которое можно предложить в начале изучения аналитической геометрии, требует рассмотрения разных вариантов расположения треугольника относительно координатных осей. Мы позволим себе здесь ограничиться только одним случаем, так как позднее (§ 5.7.) формула площади треугольника будет получена в общем случае.

Пусть треугольник расположен так, что х₁<х₃<х₂, у₁>0, у₂>0, у₃>0. Если кроме того, точка С выше прямой АВ (рис. 1.9), то S=S+S-S, где буквой S обозначается площадь треугольника или трапеции, указанных в скобках. Если точка С ниже прямой АВ, то в правой части все знаки надо сменить на противоположные. В обоих случаях S=|S+S-S|.

Подсчет площадей трапеций нетруден. Например, АСС₁А₁ есть прямоугольная трапеция с основаниями у₁ и у₃ и с высотой х₃-х₁, поэтому 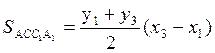. Вычисляя аналогично площади других трапеций и подставляя их в выражение для площади треугольника, получаем

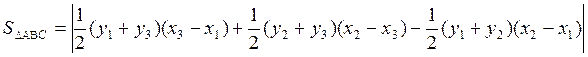 или после упрощения 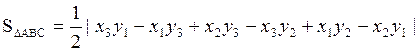. Полученную формулу площади треугольника можно записать в удобном для запоминания виде:

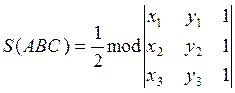                                        (1.2.5)

Здесь символ обозначает      у

абсолютную величину. Если                                С

S=0, то точки А, В, С

лежат на одной прямой.                     А

Поэтому из (1.2.5) получается                                                          В

условие коллинеарного

расположения трех точек:              O     А₁                 С₁                                           В₁                х

(рис. 1.9)

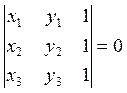                                                (1.2.6)

§ 1.3. Геометрический смысл уравнений между координатами

Мы будем рассматривать множество всех точек, координаты которых удовлетворяют некоторому уравнению. Начнем с простых примеров.

Пример 1. Уравнение у=х. Множество точек, координаты которых удовлетворяют этому уравнению, представляет собой биссектрису I и IV координатных углов (рис. 1.10).

Пример 2. Уравнение у=х². Точки, координаты которых удовлетворяют этому уравнению, образуют параболу (рис. 1.11).

Теперь рассмотрим некоторую функцию у=f(x)                                                           (1.3.1)

Каждому значению аргумента х из области определения отвечает определенное значение функции у. Если х и у рассматривать как координаты точки на плоскости, то совокупность всех таких точек образует некоторую линию - график данной функции, а уравнение (1.3.1) называют уравнением этой линии. Заметим, что часто вместо слова «линия» употребляют существительное «Кривая».

До сих пор мы рассматривали уравнения, разрешенные относительно у.  В более общем случае будем рассматривать неявное уравнение, то есть уравнение вида