Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 24

§ 3.5. Уравнение прямой с угловым коэффициентом

Определение. Уравнением прямой с угловым коэффициентом называется уравнение прямой, разрешенное относительно х, то есть уравнение вида

                                             (3.5.1)

Коэффициент k при х называется угловым коэффициентом прямой, свободный член h – ее начальной ординатой.

Общее уравнение прямой ах+bу+с=0 можно записать в виде (3.5.1) тогда и только тогда, когда в0, то есть при условии, что данная прямая не параллельна оси ординат. В этом случае .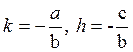

То обстоятельство, что с угловым коэффициентом можно записать уравнение не всякой прямой, является, конечно, недостатком; его  мы проиллюстрируем в конце параграфа примером 2. Достоинство же этого уравнения в том, что оно содержит не три коэффициента, как общее, а только два. Эти коэффициенты k и h имеют простой геометрический смысл, который надлежит выяснить. С этой целью введем новое понятие.

Определение. Угол, на который надо повернуть ось абсцисс в направлении оси ординат, чтобы она совпадала c данной прямой, называется углом наклона прямой к оси абсцисс; если прямая параллельна оси абсцисс или совпадает с ней, то угол наклона считается равным нулю.

Ясно, что угол наклона α заключен в пределах .

На рис. 3.11 показаны углы наклона α₁ и α₂ прямых  и .

Теорема (геометрический смысл углового коэффициента и начальной ординаты). Угловой коэффициент равен тангенсу угла наклона прямой; начальная ордината – это ордината точки пересечения прямой с осью ординат.

Доказательство. В первой части теоремы требуется доказать, что , где α – угол наклона прямой . Записав уравнение этой прямой в виде , по теореме § 3.2 находим ее направляющий вектор: . Далее надо рассмотреть три возможности.

а) . На рис. 3.12 ОА=1, АМ=k, . Из треугольника ОАМ сразу получаем: .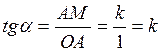

 

                       у                                                      у

 

                                                                                              М

                                                                                           k            α

                                                                          ·     α  ·        

О         А

 

                                              х                       Н

О

Рис. 3.11                                            Рис. 3.12

б) . На рис. 3.13 ОА=1, АМ=-k, . Из треугольника ОАМ имеем: 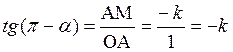, откуда по формуле привидения ..

в) . В этом случае , так как прямая  параллельна оси абсцисс и по определению .

Относительно углового коэффициента теорема доказана. Осталось выяснить геометрический смысл начальной ординаты h. С этой целью найдем координаты точки Н, в которой данная прямая пересекает ось ординат. В этой точке х=0, поэтому из уравнения прямой у=h, что и требовалось доказать.

Задача. Найти уравнение прямой, если известны ее точка А(х₀, у₀) и угловой коэффициент k.

Решение. В уравнении прямой с угловым коэффициентом (3.5.1) неизвестна только начальная ордината h. Но ее легко найти. Так как точка А лежит на прямой, то , откуда . Подставив это значение в (3.5.1), получаем  или

                        (3.5.2)

Мы получили уравнение прямой по точке и угловому коэффициенту.

Знание геометрического смысла углового коэффициента прямой позволяет вывести формулу угла между прямыми, а также условия параллельности и перпендикулярности, отличные от тех, которые были получены в § 3.3, и в ряде случаев более удобные.

Пусть две прямые  и  с углами наклона  и  и угловыми коэффициентами  и  пересекаются в точке Р (рис. 3.14). Проведем через эту точку прямую, параллельную оси абсцисс. Тогда видим, что один из углов между прямыми (на рисунке он обозначен ) равен разности углов наклона: . Найдем тангенс этого угла: 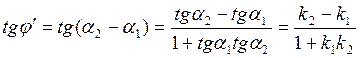. Тангенс смежного угла будет отличаться лишь знаком: . Поэтому окончательно формула угла между прямыми имеет следующий вид: