Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 6

общих точек (рис. 1.13). Общие                                              о                            х точки параболы и прямой находятся                  Рис. 1.13

из системы 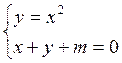 или 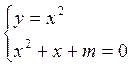. Второе уравнение системы – квадратное с дискриминантом D=1-4m.

Если D>0 (это будет при 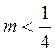), то система имеет два решения и пряма, следовательно, пересекает параболу в двух точках.

Если D=0 (это будет при 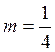), то оба решения системы совпадают и прямая касается параболы.

Если D<0 (это будет при 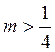), то система действительных решений не имеет и прямая, следовательно, не имеет с параболой общих точек.

§ 1.4. Уравнение окружности

Задача. Найти уравнение окружности радиуса R с центром в точке С(а, b).

          Решение. М(х, у) – произвольная точка. Она принадлежит данной окружности тогда и только тогда, когда СМ=R (рис. 1.14). Это равенство, выражающее характеристическое свойство окружности, не содержит текущих координат, поэтому его можно назвать бескоординатным уравнением окружности.

Перейдем теперь от бескоординатного уравнения к уравнению в координатной форме. Так как   то уравнение окружности имеет следующий вид: . Ввиду того, что обе его части при всех значениях переменных неотрицательны, оно равносильно такому:

                 (1.4.1)

Это и есть окончательный вид уравнения окружности. Если центр лежит в начале координат, то уравнение упрощается:

                               (1.4.2)

Мы видим, что уравнение окружности – второй степени относительно текущих координат. Выясним, в каком случае общее уравнение второй степени Ax² + Bxy + Cy² + Dx + Ey + F = 0 есть уравнение окружности. С этой целью раскроем скобки в уравнении (1.4.1): x² + y² - 2ax - 2by + (a² + b² - R²) = 0

Сравнивая оба уравнения, видим, что в уравнении окружности а) отсутствует член с произведением координат;

б) коэффициенты при квадратах переменных равны (то обстоятельство, что в уравнении окружности эти коэффициенты не просто равны между собой, а равны 1, несущественно: если уравнение окружности умножить на постоянное число, то эти коэффициенты перестанут быть равными 1, но останутся равными между собой).

Отмеченные два условия необходимы для того, чтобы уравнение второй степени было уравнением окружности. Но, как показывают примеры 5 и 6 из § 1.3 они недостаточны. Поэтому, если надо определить, является ли некоторое уравнение второй степени уравнением окружности, следует, убедившись в выполнении необходимых условий а) и б), привести уравнение к виду (1.4.1). Если при этом в правой части получится положительное число, то имеем окружность, а если отрицательное или нуль, то данное уравнение не есть уравнение окружности. Выполнив указанные операции, мы попутно определим центр и радиус окружности.

          у                                                           у     

                                          · М                                                                   М

                                                                                                                      ·

                                   С·                                                                 С · t             ·  Н

      о                                                                 о                                ·       ·          _Х

х                                           С     М₁                                                       Рис. 1.14                                                          Рис. 1.15

          Пример. Являются ли уравнения

1) х² + у² + 2х – 4у + 8 = 0

2) 3х² + 3у² + 2х – у = 0

уравнениями окружности ?

Решение. Оба уравнения – второй степени, необходимые условия а) и б) для них выполняются. Приводим уравнения к виду (1.4.1). При этом пользуемся так называемым способом выделения полных квадратов, суть которого видна из последующих выкладок, приводимых без пояснений.

1) Для первого из данных уравнений имеем:

(х² + 2х) + (у² - 4у) + 8 = 0