Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 10

              у                                                                                                у

                    М₂        М               у                                  

                                                                                                            В

В

              ·Е₂                                              М

                                                            А                                      А_1·

                                                                                                                М

                  ·                                                                                      С               ·                    А

      О       Е₁    М₁           х                О        А₁   М₁   В₁   х                     В₁                                Рис. 1.22                                  Рис. 1.23                         Рис. 1.24                                                                                                                                                                                                                   

Некоторые из полученных ранее результатов действуют в аффинных координатах, некоторые – нет.

Формула (1.2.1) длины отрезка в аффинных координатах не имеет смысл, так как здесь нет даже общей для всей плоскости единицы длины.

Формулы (1.2.3) и (1.2.4) деления отрезка в данном отношении сохраняют свое значение. Их вывод в § 1.2. остается в силе, но иллюстрируется другим чертежом (рис. 1.23).

Формула (1.2.5) площади треугольника в аффинных координатах не действует, однако ее следствие – условие (1.2.6) коллинеарного расположения трех точек – остается в силе. Но теперь оно нуждается в ином доказательстве, которое будет дано в § 2.5.

В качестве примера на использование аффинных координат докажем с их помощью известную теорему: медианы треугольника пересекаются в одной точке и делятся точкой пересечения  отношении 2 : 1, считая от вершины.

Пусть АВС – данный треугольник, АА₁ и ВВ₁ – его медианы, М –точка их пересечения (рис. 1.24). Введем систему аффинных координат, приняв за начало координат точку С, за единичный отрезок на оси ОХ – отрезок СА, на оси ОУ– отрезок СВ. Тогда А(1, 0), А₁(0, ), В(0, 1), В₁(, 0).

По формулам (1.2.3) найдем координаты точек К и L (на чертеже не показаны), которые делят отрезки АА₁  и ВВ₁ соответственно в отношении λ=2. Имеем: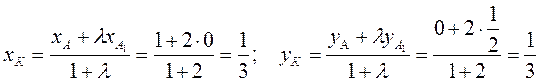

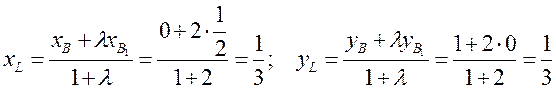
Отсюда видно, что точки К и L совпадают. Так как одна из них взята на отрезке АА₁, а другая – на ВВ₁, то обе они совпадают с точкой М. Следовательно, точка М делит обе медианы в отношении 2 : 1. так как медианы в треугольнике выбраны произвольно, то через эту же точку проходит также и третья медиана и делится ею в том же отношении.

Теорему можно было бы доказать и в прямоугольных декартовых координатах, но в этом случае выкладки были бы более громоздкими.

§ 1.8. Полярные координаты

Полярная система координат задается лучом  (полярная ось) с началом Р (полюс) и единичным отрезком РЕ. Положение каждой точки М на плоскости задается полярным радиусом S, представляющим собой длину отрезка РМ, и полярным углом РМ, отсчитываемым против часовой стрелки (рис. 1.25). Записываются полярные координаты так: М(), где  - полярный радиус,  - полярный угол. Полярный угол, если нет специальных обозначений, например, значка «о», обозначающего градусы, измеряется в радианах. По определению полярных координат . Каждой точке, кроме полюса отвечают вполне определенные полярные координаты. У полюса Р(0, -) полярный угол можно считать любым. На рис. 1.25 показаны точки Е(1, 0). А(2, ), В(1, 120⁰), С(1, 300⁰), D(2, 6).

В ряде случаев пределы изменения полярных координат не ограничивают. Тогда полярный угол любой точки имеет бесконечное множество значений, отличающихся на целое число периодов. То есть, если полярный угол равен φ, то его можно считать также равным , где k – любое целое число.