Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 18

Рассмотрим проекции вектора  на координатные оси:  и . Пусть А(х₁, у₁), В(х₂, у₂). На рис. 2.19 проекции этих точек на ось абсцисс обозначены А₁ и В₁, на ось ординат А₂ и В₂.

Будем рассматривать точки А₁ и В₁ в системе координат, которая действует на оси абсцисс: А₁(х₁) и В₁(х₂). Согласно § 1.1. разность х₂-х₁ по абсолютной величине равна длине отрезка А₁В₁, а ее знак указывает направление вектора . Следовательно эта разность есть проекция вектора . Рассуждая так же относительно проекции на ось ординат, получаем

              (2.6.2)

Но разности х₂-х₁ и у₂-у₁ по теореме 3 из § 2.4 суть координаты вектора . Это приводит нас к следующему выводу: проекции вектора на координатные оси равны его координатам. То есть, если , то

                                   (2.6.3)

Поэтому часто вместо слов «координаты вектора» говорят «проекции вектора», особенно в физике. Для этих проекций применяют обозначения а_х и а_у. Тогда .

Мы получили этот важный вывод для случая прямоугольной декартовой системы координат. Он верен и в аффинных координатах, только надо применять не ортогональное проектирование, а проектирование на одну ось в направлении другой, что иллюстрируется посредством рис. 2.20.

Теорема 1. Проекция суммы векторов равна сумме их проекций; проекция произведения вектора на число равна произведению проекции данного вектора на это число:

                          (2.6.4)

                                                 (2.6.5)

                                                 у                                     у

                              В

                                              В₂                           В                 В₂

            А                                                                                                            В

А₂          А

                                                                                             А₂              А

             А₁             В₁               о       А₁          В₁         х           о           А₁         В₁   х

Рис. 2.18                         Рис. 2.19                                  Рис. 2.20

Доказательство. Введем систему координат, приняв ось проекции  за ось абсцисс. Пусть в этой системе координат  и, следовательно, по теореме 2 из § 2.4 . Применяя дважды формулу (2.6.3), получаем: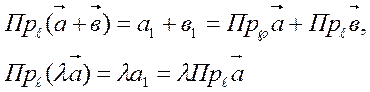

Теорема доказана. Объясните, какая нужда в этом доказательстве. Ведь справедливость теоремы, казалось бы, видна из рис. 2.21.

Определение. Пусть некоторый вектор  отложен от начала координат О оси : . Угол φ, который отсчитывается от положительного луча оси до луча ОА, называется углом вектора с осью.

Этот угол может измеряться любым действительным числом, но обычно ограничиваются его главным значением в пределах .

Теорема 2. Проекция вектора на ось равна длине вектора, умноженной на косинус угла, который вектор образует с осью.

Доказательство. Снова введем прямоугольную декартову систему координат, приняв ось проекций  за ось абсцисс. Данный вектор  отложим от начала координат:  (рис. 2.22). По определению косинуса 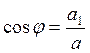 или . Применяя формулу (2.6.3), получаем

                               (2.6.6)

что и требовалось доказать.

Обратим внимание на соотношения, которые в обозначениях, использованных при доказательстве теоремы, записываются так:

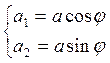                                         (2.6.7)

Первое из них только что было получено, а второе вытекает из определения синуса.

Пример. Найдите координаты вектора, получающегося поворотом вектора  на 90⁰ в положительном направлении.

 

    у                                                                                                 у

                                                               

                                                                                                х  φ

                                                                                                             О