Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 15

Рассуждения во всех четырех случаях аналогичны. Рассмотрим, например, третий. Имеем: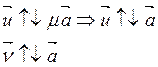                  

Итак,                   

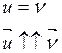
Свойство 2. (Первый дистрибутивный закон). Для любых действительных чисел λ, μ и любого вектора  верно равенство

                                (2.3.2)

Доказательство. Считаем, что , ибо в противном случае свойство выполняется тривиально.

Числа λ, μ, λ+μ могут иметь разные знаки, всего возможно 6 комбинаций:

1.                         2.

3.                        4.

5.                        6.

Доказательства во всех шести случаях аналогичны, подробно рассмотрим один из них, например, второй.

Требуется доказать равенство векторов  и .

Докажем сначала равенство длин. Так как , то .

Вычисляя длину вектора , примем во внимание, что слагаемые  и  противонаправленны. Поэтому длину вектора  находим по формуле (2.2.4): . Получили .

Докажем сонаправленность векторов  и . Так как , .

Вектор  есть сумма двух противонаправленных векторов  и , поэтому он направлен в сторону большего. Так как ,  и потому . Следовательно,  и , откуда . Итак,

        

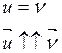
Свойство 3. (Второй дистрибутивный закон). Для любого числа λ и любых векторов  верно равенство

                       (2.3.3)

Доказательство. Полагаем , в противном случае доказываемое равенство очевидно.

а) Случай  не параллелен . Мы подробно рассмотрим доказательство при условии . Для  аналогичные рассуждения читателю предлагается выполнить самостоятельно, при этом следует воспользоваться рис. 2.12.

А₁

                                                                                                          А

          А                              В₁                       В₁                                          

                                                                                                О         В         

                        В                                                                                

О                                                                   А₁

О               Рис. 2.11                                                      Рис. 2.12

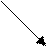
На рис. 2.11 . Обозначим через В₁ точку пересечения прямой ОВ с прямой, проходящей через А₁ параллельно АВ.

Получились два подобных треугольника ОАВ и ОАВ₁ с коэффициентом подобия λ. Поэтому А₁В₁=λАВ и ОВ₁=λОВ. Но кроме того  и , значит,  и .

С другой стороны,  и мы приходим к (2.3.3).

б) Случай . Считаем , так как в противном случае доказываемое равенство (2.3.3) превращается в тривиальное.

На основании бескоординатного признака коллинеарности существует такое число μ, что . Заменяем в обеих частях доказываемого равенства  на  и преобразуем их с учетом ранее доказанных свойств:

.

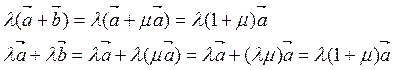Получилось одно и то же. Свойство доказано.

§ 2.4. Координаты вектора

Определение. Пусть  - векторы,  - числа, . Вектор  называется линейной комбинацией векторов , числа  - коэффициентами линейной комбинации. Представление вектора  в виде линейной комбинации векторов     называется разложением вектора  по векторам .

Теорема 1. Всякий вектор может быть единственным способом разложен по двум неколлинеарным векторам.

Доказательство. Пусть   и  - неколлинеарные векторы и  - произвольный вектор. Требуется доказать, что существуют такие числа х и у, что

                                (2.4.1)

и что эти числа определены единственным образом.

Существование. Построим векторы ,  и  из одной точки О:  (рис. 2.13). Через точку М проведем прямую параллельно прямой ОВ и точку ее пересечения с ОА обозначим М₁; аналогично на прямой ОВ строим точку М₂. В силу бескоординатного признака коллинеарности векторов существуют такие числа х и у, что . Но так как , то получаем (2.4.1)

Единственность докажем от противного: предположим, что наряду с (2.4.1) имеется другое разложение вектора  по векторам   и : .

Чтобы это разложение отличалось от (2.4.1), должно быть  или ; для определенности будем считать .