Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 19

                                                                                                         у                  х

                                                          А

          О                              х                           

Рис. 2.21                                                      Рис. 2.22

Решение. Искомый вектор обозначим . Если угол вектора а с осью абсцисс равен φ, то вектор  с этой же осью составляет угол 90⁰+φ. По формулам (2.6.7) .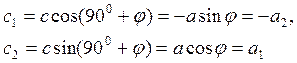

Итак, . Этот результат полезно запомнить: чтобы найти координаты вектора, полученного путем поворота данного вектора на угол +90⁰, надо поменять местами координаты данного вектора и затем изменить знак первой координаты.

§ 2.7. Скалярное произведение векторов

Определение. Углом между векторами  и  называется угол между лучами ОА и ОВ, где  , а О-произвольная точка.

Легко видеть, что от выбора точки О величина угла не зависит, то есть наше определение корректно. Согласно определению для нахождения угла между векторами надо построить их из одной точки.

Угол φ между векторами находится в пределах . Если , то φ=0, если , то φ=π.

Определение. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Скалярное произведение векторов  и  обозначается  или . По определению

                                        (2.7.1)

Подчеркнем, что скалярное произведение векторов есть число.

Скалярное произведение широко применяется не только в математике, но и в физике. Например, работа силы  на пути  равна .

Рассмотрим свойства скалярного произведения.

Свойство 1. Скалярное произведение коммутативно:

                                                (2.7.2)

вытекает непосредственно из определения.

Свойство 2. Скалярное произведение вектора на себя (так называемый скалярный квадрат вектора) равно квадрату его длины.

Действительно, . Скалярный квадрат записывают и так: . Тогда доказанное свойство выражается формулой

                                                (2.7.3)

Свойство 3. Условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

                                     (2.7.4)

В самом деле, 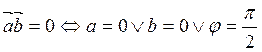. Нулевой вектор можно считать имеющим любое направление и, в частности, его можно считать перпендикулярным любому вектору (и даже самому себе!). Поэтому

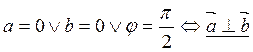
Свойство 4. Числовой множитель можно выносить за знак скалярного произведения:

                                   (2.7.5)

Доказательство. Если числовой множитель или один из векторов нулевые, то свойство выполняется тривиально. Поэтому считаем . В случае λ>0 угол между векторами  и угол между векторами  один и тот же, обозначим его φ (рис. 2.23). В этом случае (2.7.5) выполняется, так как

.

В случае λ<0 угол между векторами  обозначим тоже через φ, тогда угол между векторами  равен  (рис. 2.24). И в этом случае (2.7.5) верно, так как . Свойство доказано полностью.

Свойство 5. Скалярное произведение двух векторов равно произведению длины одного из них на проекцию другого на первый:

                               (2.7.6)

Это свойство сразу вытекает из определения скалярного произведения, если принять во внимание, что по формуле (2.6.6) будет .

Свойство 6. (Дистрибутивный закон). Скалярное произведение вектора на сумму двух векторов равно сумме скалярных произведений первого вектора на каждый из слагаемых векторов:

                                  (2.7.7)

Имеем: .

Здесь знаки равенства 1 и 4 поставлены на основании свойства 5, знак 2 – на основании формулы (2.6.4). Обратите внимание на знак равенства 3. В левой части этого равенства число а множится на сумму чисел  и , и мы воспользовались дистрибутивным законом для чисел.

Свойство 7. (Выражение скалярного произведения через координаты). Скалярное произведение двух векторов равно сумме произведений соответствующих координат:

                                     (2.7.8)

где