Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 11

Отрицательный полярный радиус откладывается в противоположном направлении, то есть при перемене знака у полярного радиуса полярный угол изменяется на . При таком обобщении, например, координатами точки С на рис. 1.25 можно считать (-1, 120⁰). Последнее обобщение применяется реже.

Примем полюс за начало прямоугольной декартовой системы координат, полярную ось – за положительный луч оси абсцисс, а положительный луч оси ординат проведем под углом +90⁰ к полярной оси (рис.  1.26). Тогда координаты всякой точки М можно определить в двух системах координат: М(ρ, φ)- в полярной, М(х, у) – в декартовой. Найдем связь между полярными и декартовыми координатами точки.

Если точка М находится в первом координатном углу, то из треугольника РММ₁, где М₁ – проекция точки М на ось абсцисс, имеем

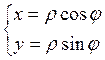                                (1.8.1)

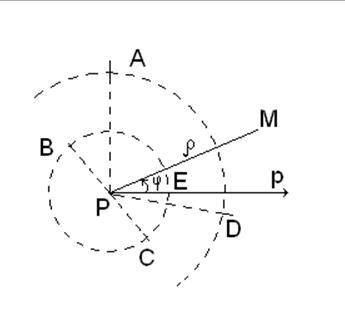
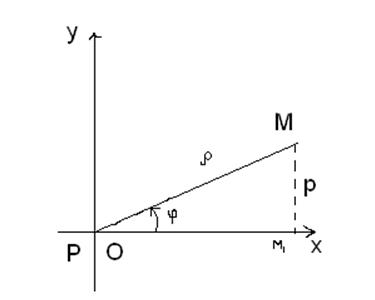
Рис. 1.25                                                      Рис. 1.26

На самом деле эти формулы верны при любом положении точки М, ибо общее определение синуса и косинуса в наших обозначениях таково: .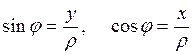

Уравнение (1.8.1) можно разрешить относительно полярных координат, то есть выразить их через декартовы. С этой целью разделим второе уравнение на первое: 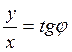; теперь возведем оба уравнения почленно в квадрат и сложим: . Итак,

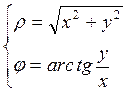                            (1.8.2)

При пользовании второй из этих формул надо по знакам х и у определить координатный угол, в котором находится точка. В противном случае при вычислении полярного угла возможна ошибка на период тангенса 180⁰.

Пример 1. Найдите полярные координаты точки А(-1, -), заданной прямоугольными декартовыми координатами.

Решение. По формулам (1.8.2)

.

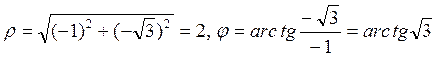Так как точка А находится в третьем координатном углу, то φ=240⁰. Итак, в полярных координатах А(2, 240⁰).

Пример 2. Уравнение φ=α – это уравнение луча, образующего угол α с полярной осью.

Пример 3. Уравнение ρ=а – это уравнение окружности радиуса а с центром в полюсе.

Пример 4. Уравнение окружности (1.4.1) в силу формул (1.8.1) в полярных координатах имеет вид  или после преобразований, .

Пример 5. Линия, для всех точек которой полярный радиус и полярный угол пропорциональны, называется спиралью Архимеда. Уравнение спирали:  где .

На рис. 1.27 изображена спираль Архимеда .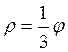

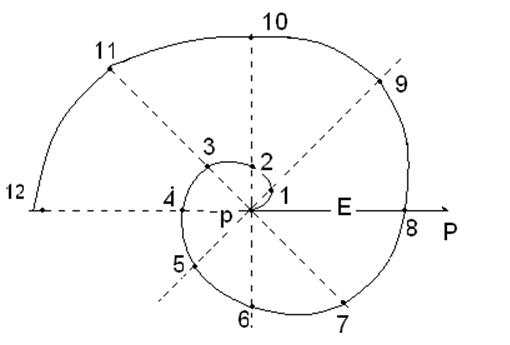
Рис. 1.27

На ней отмечены точки, координаты которых даны в следующей таблице:

	1	2	3	4	5	6	7	8	9	10	11	12

ГЛАВА 2. ВЕКТОРЫ НА ПЛОСКОСТИ

§ 2.1. Определение вектора

Определение. Вектором называется направленный отрезок, то есть отрезок, для которого указаны начало и конец. Если начало и конец вектора совпадают, то такой вектор называется нулевым. Длина отрезка называется длиною  или модулем вектора.

Обозначается вектор как отрезок, но вверху ставится стрелка: ; тот же вектор можно обозначить одной какой-либо буквой, например, . В книгах для упрощения набора стрелку часто не применяют, но букву набирают жирным шрифтом: u. Обозначения длины того же вектора: ;  - нулевой вектор, .

Определение. Два вектора называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Коллинеарность векторов обозначается так же, как параллельность прямых: . Ясно, что нулевой вектор коллинеарен любому: .

Для последующих определений необходимо вспомнить понятие сонаправленности лучей.

Определение. Пусть имеются лучи h и k с началами Н и К соответственно. Если эти лучи не лежат на одной прямой, то они называются сонаправленными в случае, когда они параллельны и лежат по одну сторону от прямой НК (рис. 2.1.а). Если лучи лежат на одной прямой, то они называются сонаправленными, если один из них – часть другого (на рис. 2.1б kh). Если лучи параллельны или лежат на одной прямой, но не сонаправлены, то они называются противонаправленными.