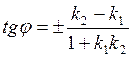 (3.5.3)
(3.5.3)
![]() у
у
 |
Н ![]()
![]()
![]() α α х
α α х
 |
О
![]()
М
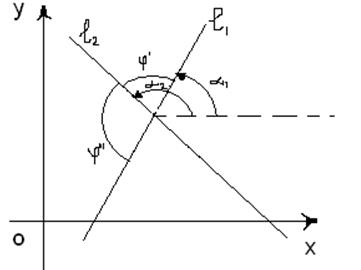
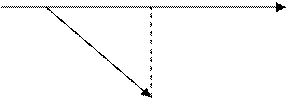
Рис. 3.13 Рис. 3.14
Из
этой формулы выведем условия параллельности (допускается и совпадение) и
перпендикулярности прямых: ![]()
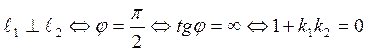 .
.
Итак, условием параллельности прямых является равенство их угловых коэффициентов:
![]() (3.5.4)
(3.5.4)
а условие перпендикулярности, имеющее вид
![]() (3.5.5)
(3.5.5)
удобно запомнить в такой форме: угловые коэффициенты перпендикулярных прямых обратны по величине и противоположны по знаку.
Пример
1. Найти уравнения биссектрис углов
между прямыми ![]() и
и ![]() .
.
Эта задача уже дважды решалась: в § 3.2. и § 3.4.
Решение.
а) Решая совместно уравнения данных прямых, находим точку их пересечения: 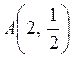 .
.
б)
Неизвестный угловой коэффициент биссектрисы обозначим k, угловые коэффициенты
данных прямых находим из их уравнений: 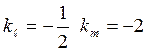 . Так
как биссектриса образует равные углы с прямыми
. Так
как биссектриса образует равные углы с прямыми ![]() и
и ![]() , то по формуле (3.5.3)
, то по формуле (3.5.3) 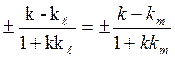 . Получилось уравнение с одним неизвестным k.
Оно равносильно совокупности двух уравнений:
. Получилось уравнение с одним неизвестным k.
Оно равносильно совокупности двух уравнений: 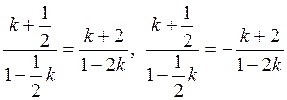 ,
которые после упрощений принимают вид
,
которые после упрощений принимают вид ![]() .
.
Первое
не имеет действительных решений, а из второго получаем два значения углового
коэффициента - ![]() .
.
в)
Находим уравнения биссектрис по точке А и угловому коэффициенту (формула (3.5.2)):
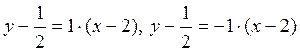 и окончательно
и окончательно ![]()
![]() .
.
Пример 2. Найти уравнения касательных, проведенных из точки А(1, 2) к окружности х2 + у2 = 1.
Решение.
Радиус данной окружности равен 1, расстояние от точки А до ее центра О
равно ![]() . Так как
. Так как ![]() >1,
то точка А лежит вне круга и из нее можно провести две касательные к
окружности.
>1,
то точка А лежит вне круга и из нее можно провести две касательные к
окружности.
Уравнения
прямых, проходящих через точку А запишем по точке и переменному угловому
коэффициенту k: у – 2 = k(x - 1). Касательные
выделяются из этого множества прямых по такому признаку: они и только они имеют
с окружностью одну общую точку. Таким образом, надо найти те значения k,
при которых система 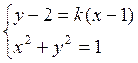 или
или 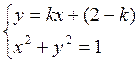 имеет
единственное решение.
имеет
единственное решение.
Исключая
у, получаем уравнение относительно х: ![]() . После
упрощений оно принимает вид
. После
упрощений оно принимает вид ![]() .
.
Касательным
соответствуют те значения k, при которых это квадратное уравнение имеет одно
решение, то есть те, при которых дискриминант равен нулю: ![]() .
.
Поскольку
в ответе должны получиться две касательные, можно было ожидать, что после
раскрытия скобок и привидения подобных членов получится уравнение второй
степени. Однако получаем ![]() , откуда
, откуда 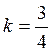 . Зная угловой коэффициент, находим
касательную:
. Зная угловой коэффициент, находим
касательную: 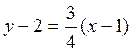 или
или ![]() .
.
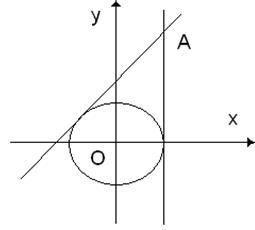 А
где же вторая касательная? Теперь пора вспомнить, что пользуясь уравнением
прямой с угловым коэффициентом, мы не учитываем прямые, параллельные оси
ординат. Не будет ли прямая, проходящая через точку параллельно оси ординат,
касательной к данной окружности? Уравнение такой прямой у – 1 = 0, она отстоит
от начала координат, то есть от центра окружности, на расстояние 1 и поэтому
касается данной окружности (рис. 3.15) Итак, получилось два решения: 3х – 4у +5
= 0. у – 1 = 0.
А
где же вторая касательная? Теперь пора вспомнить, что пользуясь уравнением
прямой с угловым коэффициентом, мы не учитываем прямые, параллельные оси
ординат. Не будет ли прямая, проходящая через точку параллельно оси ординат,
касательной к данной окружности? Уравнение такой прямой у – 1 = 0, она отстоит
от начала координат, то есть от центра окружности, на расстояние 1 и поэтому
касается данной окружности (рис. 3.15) Итак, получилось два решения: 3х – 4у +5
= 0. у – 1 = 0.
Рис. 3.15
§ 3.6. Пучок прямых
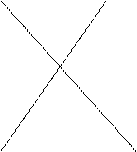
Определение. Собственным пучком прямых называется множество прямых, проходящих через одну точку – центр пучка (рис. 3.16); несобственным пучком называется множество параллельных между собой прямых (рис. 3.17)
Собственный пучок может быть задан центром, несобственный – одной из своих прямых. Вообще же, любой пучок можно задать двумя его прямыми – образующими пучками, причем в качестве образующих можно взять любые прямые пучка. При этом нет надобности указывать вид пучка. Располагая образующими, мы можем через любую точку плоскости, исключая центр в случае собственного пучка, однозначно провести прямую пучка.
 |

![]()
![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.