Итак, для того, чтобы две прямые были параллельными или совпадающими, необходимо и достаточно, чтобы в их уравнениях коэффициенты при текущих координатах были пропорциональны:
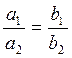(3.3.2)
а для того, чтобы прямые были перпендикулярны, необходимо и достаточно, чтобы сумма произведений коэффициентов при соответствующих координатах равнялась нулю:
(3.3.3)
Интересно
и поучительно рассмотреть вопрос о взаимном расположении прямых (и, в
частности, вывести условие параллельности) из алгебраических соображений.
Поставим вопрос так: сколько общих точек имеют данные прямые? Число общих точек
двух прямых равно числу решений системы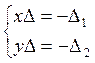 
где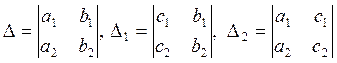 
.
Отсюда
видим, что при 
система имеет единственное
решение, то есть прямые пересекаются. Если же 
, но при
этом 
или 
, то
система решений не имеет и прямые, следовательно, параллельны. При 
система имеет бесконечное множество
решений, а это означает, что прямые совпадают.
Известно, что определитель второго порядка равен нулю, тогда и только тогда, когда его строки пропорциональны. Поэтому результаты исследования можно представить в такой форме:
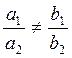- прямые пересекаются;
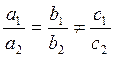- прямые параллельны;
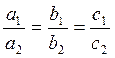- прямые совпадают.
Еще раз видим, что при условии (3.3.2) прямые параллельны или совпадают.
§ 3.4. Расстояние от точки до прямой
Задача.
Найти расстояние от точки А(х0, у0) до прямой 
.
Решение.
Из точки А опустим перпендикуляр АК на прямую 
(рис.
3.9); d=АК – искомое расстояние. Для его нахождения поступим так: а) найдем уравнение
прямой АК; б) найдем координаты точки К; в) найдем d.
· А
m
d
К Рис. 3.9 Рис. 3.10
а)
Нормальный вектор 
прямой является
направляющим вектором прямой АК, то есть 
. Это
позволяет записать уравнение прямой АК по точке А и направляющему вектору (а,
в) по формуле (3.1.1):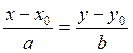 
или в параметрическом
виде (3.1.3):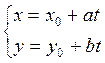 
.
б)
Находим точку К, для чего решаем систему, составленную из уравнений прямых и АК: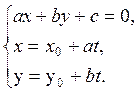 
. С
этой целью исключаем из системы х и у, что позволяет найти t –
значение параметра, соответствующее точке К. Имеем: 
,
откуда 
и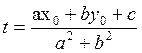 
.
Координаты
точки К получим теперь, подставив найденное значение t во второе и
третье уравнения системы: 
.
в)
Находим искомое расстояние: 
. Подставляем сюда найденное выше значение t:
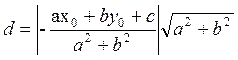и после очевидных упрощений получаем
окончательный результат:
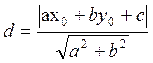(3.4.1)
Вывод: расстояние от точки до прямой равно дроби, в числителе которой стоит абсолютная величина того значения, которое принимает левая часть общего уравнения данной прямой, если в нее вместо текущих координат подставить координаты данной точки, а в знаменателе – корень квадратный из суммы квадратов коэффициентов при текущих координатах.
Пример 1. Найдите расстояние от точки А(5,1) до прямой 3х-4у-1=0.
Решение.
По формуле (3.4.1)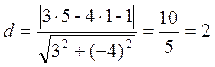 
.
Пример
2. Найдите уравнения биссектрис углов между прямыми 
и
. Этот пример уже решался, см. § 3.2.
Решение.
Все точки N(х, у), лежащие на одной из биссектрис, и только они,
равноудалены от прямых и m (рис. 3.10).
Согласно формуле (3.4.1) ее расстояния до этих прямых равны соответственно 
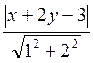и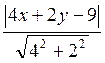 
.
Поэтому
уравнение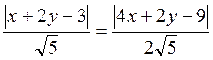 
есть уравнение пары биссектрис. Оно
равносильно совокупности двух уравнений первой степени
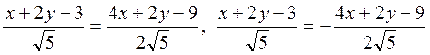или после упрощений 2х-2у-3=0,
2х+2у-5=0. Это и есть уравнения искомых биссектрис.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.