Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 21

а) Найдем уравнение прямой, проходящее         через точки А(х₁, у₁) и В(х₂, у₂).

Так как вектор  есть направляющий вектор данной прямой, то ее уравнение с помощью формулы (3.1.1) можно записать по точке А и направляющему вектору :

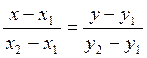                                   (3.1.2)

Мы получили уравнение по двум точкам.

Уравнение той же прямой можно было записать по точке В и направляющему вектору : 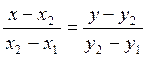. Легко показать. Что оба уравнения совпадают.

б) В § 1.3 мы видели, что уравнения линий могут быть записаны в параметрической форме. Для этого надо координаты текущей точки (х, у) данной линии выразить через одну переменную, называемую параметром.

Обе части уравнения (3.1.1), представляющие собой равные переменные величины. Примем за параметр t: .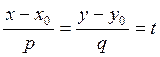

Через этот параметр выразим текущие координаты:

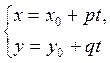                                         (3.1.3)

Мы получили параметрические уравнения прямой.

Определение. Ненулевой вектор называется нормальным вектором прямой, если он ей перпендикулярен.

Всякая прямая имеет бесконечное множество нормальных векторов, но они все коллинеарны между собой. Значит, если  - нормальный вектор прямой, то всякий нормальный вектор этой прямой можно записать в виде , где .

Задача 2. Найти уравнение прямой  по точке А(х₀, у₀) и нормальному вектору (а, b).

Решение. Пусть М(х. у) – какая-либо точка (рис. 3.3). Тогда  и .

Мы получили уравнение прямой по точке и нормальному вектору:

                         (3.1.4)

В дальнейшем мы закрепим использованные обозначения направляющего () и нормального () векторов прямой. При необходимости будем употреблять и более подробные обозначения. Например,  - это направляющий вектор прямой m, а равенство  показывает, что направляющий вектор прямой m является в то же время нормальным вектором прямой KL. И т.д.

Пример. Даны вершины треугольника: А(-3, 1), В(2, 4), С(0, -5). Найдите уравнение стороны ВС и высоты, проведенной из вершины А.

 

                                                                                                А         

                                                                                                                                                                                                                          

                    М                                                                           

       А                                                           В                                   С

Рис. 3.3                                                                      Н  

Рис. 3.4                                                                               Примечание. Мы считаем допустимым здесь и в других подобных случаях неполные формулировки, так как полные довольно громоздки. Например, в данном случае вопрос задачи надо было бы сформулировать так: найдите уравнение прямой, содержащей сторону ВС, и уравнение прямой, содержащей высоту, проведенную из вершины А.

Решение. Так как , где АН – высота (рис. 3.4), то по формулам (3.1.1) и (3.1.4) соответственно имеем: 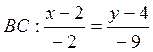, . После упрощений получаем окончательные ответы: .

§ 3.2. Общее уравнение прямой

Полученные выше уравнения прямой по точке и направляющему вектору (3.1.1) и по точке и нормальному вектору (3.1.4) показывают, что уравнение  всякой прямой есть уравнение первой степени относительно текущих координат х и у. Верно ли обратное утверждение? Положительный ответ на этот вопрос дает следующая теорема.

Теорема. Всякое уравнение первой степени

                 (3.2.1)

относительно текущих координат есть уравнение прямой. Вектор  является нормальным вектором этой прямой, вектор  - направляющим.

          Доказательство. Обозначим буквой  линию, уравнение которой имеет вид (3.2.1):  (рис. 3.5) и возьмем на ней произвольную точку, например, точку 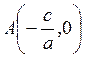.                                                         у                  ах+bу=0

                                                                     х=0