Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 13

                                                            А                     

                                       В        О   ·                       ·                              О ·                                                                                               

О              Рис.2.5                                              В      

                                                         В

 

                                                                                                            В₁

 

                                                            А                  

                                                                                            А₁

               О              К                                                                                 

                                                                             О

Рис. 2.6                                              Рис. 2.7                         О₁

Доказательство запишем символически:

            

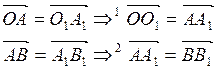
В местах, отмеченных цифрами 1, 2, 4 применена теорема предыдущего параграфа, стрелка 3 поставлена на основании транзитивности равенства векторов. Теорема доказана.

Рассмотрим свойства сложения векторов.

Свойство 1. Модуль суммы двух векторов не превосходит сумму их модулей:

                                        (2.2.2)

Если , то из треугольника ОАВ (рис. 2.5а) OB<OA+AB, то есть

                                        (2.2.3)

Если , то OB=OA+AB (рис. 2.5б) и потому

                                        (2.2.4)

Если , то OB=|OA-AB| (рис. 2.5в) и потому

                                                 (2.2.5)

Как видим, неравенство (2.2.2) верно во всех случаях.

Доказанное свойство можно сформулировать более детально: модуль суммы двух неколлинеарных векторов меньше суммы их модулей; модуль суммы двух коллинеарных векторов равен сумме или абсолютной величине разности модулей этих векторов, смотря по тому, сонаправлены или противонаправлены слагаемые. Заметим также, что сумма двух коллинеарных векторов всегда направлена в сторону большего (по длине) слагаемого.

Свойство 2.        

                    (2.2.6)

В самом деле, если , то по правилу треугольника (2.2.1)

 и

Свойство 3. Сложение векторов коммутативно:

                                         (2.2.7)

Доказательство. Пусть сначала . От произвольной точки О отложим векторы  и . Через А проведем прямую параллельно ОВ, через В – параллельно ОА, С – точка их пересечения. Получился параллелограмм ОАСВ (рис. 2.8). По правилу треугольника (2.2.1) имеем:

, откуда и вытекает требуемое.

Пусть теперь . Тогда длины векторов  и  выражаются в случае  формулой (2.2.4), а в случае  - (2.2.5), но в обоих случаях будет . Кроме того, , так как оба эти вектора сонаправлены с большим из векторов  и . По определению равенства отсюда следует (2.2.7).

На доказанном свойстве основан способ сложения двух векторов, называемый правилом параллелограмма. Суть его видна из того же рис. 2.8. Параллелограмм ОАСВ называют параллелограммом, построенным на векторах  и .

Свойство 4. Сложение векторов ассоциативно:

                           (2.2.8)

Доказательство. Возьмем произвольную точку О и построим векторы ,  (Рис. 2.9.). Тогда по правилу треугольника

 и далее

Из последних двух равенств следует (2.2.8).

Определение. Вектор  называется разностью векторов   и , если его сумма с вектором  равна .

Это определение означает, что формулы  и  выражают одно и то же.

На рис. 2.10 , . Так как , то по определению . Отсюда вытекает правило: чтобы построить разность двух векторов, надо построить эти векторы из одной точки и конец второго соединить с концом первого.

Свойство 5. Векторы  и  противоположны:

                                     (2.2.9)