Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 26

                   ·                                                                                                  

                                                                                                                      А

 

                                                                                             

Рис. 3.16                              Рис. 3.17                                       Рис. 3.18

Аналитически множество прямых задается уравнением первой степени, но с переменными коэффициентами. По существу мы уже встречались с уравнениями пучков. Например, уравнение (3.1.1) прямой по точке и направляющему вектору при переменных p  и q есть уравнение собственного пучка с центром (х₀, у₀), а при переменных х₀ и у₀ – уравнение несобственного пучка прямых, параллельных вектору . Аналогично как уравнения собственного и несобственного пучков могут рассматривать уравнение прямой (3.1.4) по точке и нормальному вектору и уравнение прямой (3.5.2) с угловым коэффициентом. Последнее уравнение при переменном k представляет собой уравнение собственного пучка, из которого исключена прямая, параллельная оси ординат.

Теорема. Пусть имеется пучок прямых с образующими

 тогда уравнение

                (3.6.1)

где λ – переменное, есть уравнение этого пучка, из которого  исключена прямая .

Уравнение пучка (3.6.1) будем записывать и в другой форме:

             (3.6.2)

Доказательство. Состоит из четырех частей.

1). При любом λ (3.6.1) есть уравнение первой степени относительно текущих координат. Это значит, что (3.6.1) – уравнение множества прямых.

2). Если прямые  и  пересекаются, то любая прямая из множества (3.6.1) проходит через точку пересечения, то есть прямые (3.6.1) при любом λ входят в один собственный пучок. В самом деле, если (х₀, у₀) – точка пересечения образующих  и , то есть , то координаты этой точки удовлетворяют уравнению (3.6.1) при любом значении λ.

3). Если  || , то есть для образующих выполняется условие параллельности 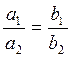, то любая прямая (3.6.2) параллельна образующим  и , то есть при любом λ все прямые (3.6.2) входят в один несобственный пучок. Докажем это.

Чтобы прямые (3.6.2) были параллельны, например, прямой , должно выполняться условие 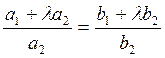. И оно действительно выполняется, так как .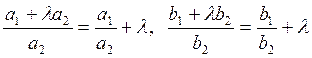

4). Итак, уже доказано, что все множество прямых (3.6.1) входит в один пучок. Осталось доказать, что в это множество входят все прямые данного пучка, за исключением прямой .

Для доказательства возьмем в пуске какую-либо прямую , отличную от  (рис. 3.18), и покажем, что ее уравнение имеет вид (3.6.1) при некотором значении λ.

На прямой  возьмем произвольно точку  и ее координаты подставим в (3.6.1): .

Принимая во внимание, что , отсюда получаем:

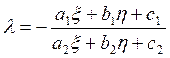. Если это значение λ подставить в уравнение (3.6.1), то получим уравнение прямой. Эта прямая, во-первых, проходит через точку А, так как координаты этой точки  удовлетворяют полученному уравнению. Во-вторых, в соответствии со второй и третьей частями доказательства это будет уравнение прямой пучка. Следовательно, мы получили уравнение прямой .

Теорема доказана. Чтобы не делать в ней оговорки об исключении прямой , уравнение пучка можно записать в таком виде

            (3.6.3)

где  и  - переменные. Уравнение стало несколько менее удобным для решения задач, так как в нем теперь два переменных параметра. Зато оно описывает весь пучок. В частности, при  получается прямая , а при  - прямая .

Пример. Через точку пересечения прямых 2х – у + 3 = 0 и х + 3у – 1 =0 проведены прямые  и m причем  и  где . Найдите уравнения прямых  и m.

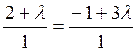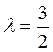Решение. Этот пример мог быть рассмотрен и в § 3.1. Здесь мы решим его, используя уравнение пучка (3.6.1). Искомые прямые входят в пучок  или . Так как , то по условию (3.3.2) параллельности прямых , откуда . Внося это значение в уравнение пучка, получаем уравнение прямой .

Так как , то по условию (3.3.3) перпендикулярности прямых , откуда . Внося это значение в уравнение пучка, получаем уравнение прямой .